Vediamo il recap delle puntate precedenti:
- puntata 0: "Viaggio nell'≪immaginario≫ mondo dei numeri complessi";
- puntata 1: "Primi elementi di analisi complessa: le condizioni di olomorfismo di Cauchy-Riemann";- puntata 2: "Introduzione all'integrazione complessa";
- puntata 3: "La rappresentazione integrale di Cauchy";
- puntata 5: "Analisi complessa: zeri e singolarità";
- puntata 6: "La classificazione delle funzioni monodrome";
- puntata 7: "Analisi complessa: residui";
- puntata 8: "Il valore principale di Cauchy";
- puntata 9: "Analisi complessa: lemma di Jordan e lemmi minori";
- puntata 10: "Il prolungamento analitico e le funzioni polidrome".
Questa puntata è dedicata a 2 particolari funzioni introdotte da Eulero (1707-1783) e, al fine di illustrarle, faremo uso di alcuni dei concetti spiegati nei post passati.
Cominciamo dicendo che nel 1727 Eulero venne chiamato da Daniel Bernoulli a ricoprire una cattedra di medicina prima, e matematica poi, presso l'Accademia delle Scienze di San Pietroburgo.
I 2 divennero stretti collaboratori fino alla dipartita di Bernoulli nel 1733.
L'autodidatta Christian Goldbach era anch'egli, in quegli anni, professore presso la suddetta Accademia.
Pare che fu proprio Goldbach a proporre ad Eulero di trovare una funzione che estendesse il fattoriale ai numeri non interi.
Ne seguì una corrispondenza tra i 2 (che continuò poi su innumerevoli questioni per ben 35 anni) durante la quale, in una celebre lettera di Eulero a Goldbach del 13 ottobre 1729, comparve per la prima volta la funzione gamma sotto forma di limite di un prodotto e di prodotto infinito:
Questa è appunto la cosiddetta rappresentazione di Eulero per la funzione gamma.
Esso converge uniformemente per Re(z) > 0, definendo perciò una funzione analitica nel semipiano destro, in quanto dotata di derivata prima univocamente definita e in tal semipiano non si annulla mai.
Dalla definizione segue immediatamente che, in particolare, Γ(1) = 1.
Effettuiamo un'integrazione per parti, scegliendo come fattore differenziale
(è possibile scegliere senza problemi anche il fattore e-t dt).
Abbiamo innanzitutto che:
da cui si ricava:
La parte già integrata è chiaramente nulla per Re(z) > 0, mentre il nuovo integrale rappresenta la funzione Γ(z+1).
Ergo, la funzione Γ soddisfa l'equazione alle differenze finite:
che è l'equazione fondamentale per la funzione gamma.
Iterando la suddetta equazione si ottiene la relazione
ove n è un numero naturale qualsiasi.
In particolare, per z = 1, si ha

La funzione Γ avente per argomento un numero intero positivo coincide perciò con un fattoriale e la formula

mostra che, in un certo senso, la funzione Γ(z) può considerarsi come l'estensione del concetto di fattoriale a numeri complessi arbitrari (proprio quello che Goldbach aveva chiesto ad Eulero!).
Nella letteratura la funzione gamma viene talvolta indicata pure col simbolo di fattoriale, ossia ∏, intendendosi:
L'espressione
consente poi di determinare il comportamento analitico di Γ(z) nel semipiano Re(z) < 0.
Infatti Γ(z+n) risulta olomorfa nel semipiano Re(z) > -n e quindi, riscrivendo la formula di prima come
si nota che i punti z = 0, z = -1, ..., z = -n + 1 sono poli semplici di Γ(z).
Data l'arbitrarietà di n, è possibile concludere che la funzione Γ(z) possiede un'infinità di poli semplici nei punti z = -k, con k = 0, 1, 2,....
Inoltre, l'unica ulteriore singolarità di Γ(z) è il punto all'infinito, che è una singolarità essenziale (non isolata, giacché punto di accumulazione di poli).
Tirando le fila del discorso, Γ(z) è dunque una funzione meromorfa.
Di seguito il grafico della funzione gamma:
La formula
permette anche una valutazione immediata dei residui di Γ(z) nei punti z = -k.
Considerando il polo situato in z = -n +1, si ha
e quindi, vista l'arbitrarietà di n, si ricava:
La formula
mostra pure che Γ(z) è una funzione senza zeri, visto che la funzione a 2° membro è palesemente priva di zeri, per qualsiasi valore di n.
La funzione inversa, 1/Γ(z), è perciò una funzione intera.
Osserviamo ora che, utilizzando la funzione Γ(z) sulla base dell'equazione alle differenze finite, si può giungere ad un'espressione compatta per il coefficiente binomiale, il quale, per valore arbitrari di z, è definito come:
Moltiplicando e dividendo per Γ(z - k +1), sempre tenendo conto dell'equazione alle differenze finite, si vede subito che:
Ovviamente, per z = n (intero positivo), il tutto si riduce, ricordando che Γ(n+1) = n!, alla classica espressione
Un'importante funzione, imparentata con la funzione Γ, è la funzione beta di Eulero, indicata col simbolo B(p, q), la quale è definita attraverso "l'integrale euleriano di I tipo", dovuto a Legendre:
con Re(p) > 0, Re(q) > 0.
Essa è simmetrica rispetto allo scambio di p con q, come si nota banalmente dalla sua formula effettuando il cambiamento di variabile t' = 1 - t.
La funzione beta risulta esprimibile in termini di funzioni Γ come:
Per mostrare la validità di questa relazione, iniziamo a costruire una nuova rappresentazione integrale per Γ(z), ottenuta da
ponendo t = x²:
Andiamo a scrivere pertanto il prodotto Γ(p)Γ(q) facendo uso della nuova rappresentazione di Γ:
Passando, nel piano xy, alle coordinate polari (x = R cos φ, y = R sin φ), ne segue:
Nell'integrale in dR si può riconoscere la funzione Γ(p+q)/2, grazie alla rappresentazione di Γ(z) che avevamo ottenuto ponendo t = x², e quindi abbiamo che:
Da ciò segue facilmente la validità della relazione
giacché il 2° membro della precedente equazione si riduce, effettuando il cambio di variabile cos² φ = t, all'integrale che abbiamo assunto come definizione della funzione beta.
Esso costituisce pertanto, a sua volta, una possibile rappresentazione della suddetta funzione:
Un'altra rilevante relazione è la seguente:
Tale uguaglianza è valida in tutto il piano complesso.
Entrambi i membri sono definiti in tutto il piano complesso, eccetto i poli semplici situati nei punti z = 0, ±1, ±2,....
La suddetta espressione risulta inoltre equivalente alla relazione
essendo Γ(1-z) = -zΓ(-z).
Definiamo ora la cosiddetta rappresentazione di Hankel per la funzione gamma come:
la quale definisce la funzione Γ(z) per ogni valore finito di z e con c opportuno cammino.
Naturalmente tutte le proprietà di Γ(z), che abbiamo già ottenuto partendo dalla rappresentazione originaria, si potrebbero riottenere pure dalla rappresentazione di Hankel.
Per la funzione gamma vale poi la formula di duplicazione:
Per quanto concerne l'andamento asintotico, per grandi valori di |z|, della funzione Γ(z), vale la formula di Stirling:
Se ricordate, avevamo già introdotto la formula di Stirling, relativamente a n!, qui.
Una notevole conseguenza di tale formula è la relazione
quando z → ∞.
Essa fornisce il comportamento asintotico del rapporto di 2 funzioni Γ i cui argomenti tendono ad infinito, mantenendo costante la loro differenza.
Giusto per completezza, osserviamo un'ulteriore rappresentazione della funzione gamma denominata rappresentazione di Weierstrass:

dove γ designa la cosiddetta costante di Eulero-Mascheroni.
Terminiamo la narrazione con una piccola curiosità.
Nel 1968 il fisico italiano Gabriele Veneziano, sfruttando proprio la funzione beta di Eulero, introdusse la nozione di ampiezza di Veneziano, una grandezza fisica che è possibile interpretare come una particolare ampiezza di scattering relativa a una determinata sezione d'urto.
Ma perché tutto ciò risulta così importante?
Ebbene, l'introduzione di questo singolare concetto fu alla base della nascita di una delle teorie fisiche più affascinanti del XX secolo (ma ancora priva di verifica sperimentale): la teoria delle stringhe.
Infatti, Leonard Susskind, John Schwarz e Yōichirō Nambu arrivarono a teorizzare, prendendo come riferimento il lavoro di Veneziano, l'originale fenomeno di urto tra le stringhe.
Per gli interessati, ho fornito un'introduzione davvero molto semplice ed accessibile (adatta pure a un lettore senza grande formazione scientifica) alla teoria delle stringhe sul blog Al Tamburo Riparato (cliccate qui)
Siamo giunti alla conclusione del nostro lungo viaggio dedicato ad impartire i rudimenti dell'analisi complessa.
Mi auguro che questa lunga serie di post possa essere stata d'aiuto al lettore (con qualche base di analisi matematica) ad avventurarsi dolcemente nell'affascinante, ma non semplice, mondo delle funzioni di variabile complessa.






















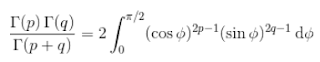




























Nessun commento:
Posta un commento