Andiamo ora ad introdurre uno dei concetti fondamentali della meccanica statistica, il cosiddetto teorema di equipartizione dell'energia, per poi osservare come si applica ad un noto fenomeno, studiato anche da Einstein nel 1905, ovvero il moto browniano.
Sin da subito avvertiamo il lettore che il suddetto teorema fornisce una semplice e chiara teoria dei sistemi termici, ma resta buono solo considerando elevate temperature; in tal caso è infatti possibile trascurare senza problemi i particolari dei livelli energetici quantizzati.
Non è raro in fisica trovarsi di fronte alla dipendenza dell'energia dal quadrato di una certa variabile.
L'esempio più semplice a cui si può pensare è quello dell'energia cinetica K di una particella di massa m e velocità v:

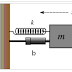
 Un altro bell'esempio è fornito dall'energia potenziale U di una massa sospesa ad una estremità di una molla (avente costante elastica k) e spostata di una distanza x dal suo punto di equilibrio:
Un altro bell'esempio è fornito dall'energia potenziale U di una massa sospesa ad una estremità di una molla (avente costante elastica k) e spostata di una distanza x dal suo punto di equilibrio:
Naturalmente l'energia totale E della massa in moto all'estremità della molla è la somma dei 2 termini appena citati:
È poi chiaro che se la massa subisce un moto armonico semplice, l'energia viene scambiata tra K ed U, ma l'energia totale E rimane costante.
Generalizziamo ora il discorso e supponiamo di star considerando un sistema la cui energia presenti una dipendenza quadratica (rispetto a una certa variabile) e che sia in grado di interagire con un serbatoio termico.
Per chi non ricordasse, un serbatoio termico (in inglese detto reservoir o heat bath) è un oggetto che poniamo avere una capacità termica infinita.
Siccome la capacità termica è definita, in generale, come il rapporto tra il calore Q scambiato tra il corpo preso in esame e l'ambiente e la conseguente variazione di temperatura ΔT, una capacità termica infinita significa (assumendo che Q sia finito) che ΔT tende a 0.
Ciò equivale a dire che se anche sottraessimo un'ingente quantità di energia al serbatoio, non si avrebbe praticamente alcuna variazione di temperatura.
Ricordiamo pure, per completezza, che le situazioni in cui abbiamo a che fare con un piccolo sistema che interagisce con un reservoir sono molti comuni nell'ambito della termodinamica e vengono chiamate ensembles canonici.
L'energia E del nostro piccolo sistema sarà descritta dalla facile legge:

ove α denota una qualche costante positiva ed x una qualche variabile.
Supponiamo poi che x possa, in linea di principio, assumere qualsivoglia valore con eguale probabilità.
Ne consegue che la probabilità P(x) del sistema di avere una particolare energia αx² risulta proporzionale al fattore di Boltzmann e-βαx², dove β = 1/kBT, con kB costante di Boltzmann e T temperatura del serbatoio.
Andando a normalizzare (ossia assicurarsi che la somma su tutte le probabilità sia 1) l'espressione, avremmo:

e l'energia media potrà essere data da:

Un risultato sicuramente interessante, dato che è indipendente dalla costante α e pone in evidenza la diretta proporzionalità sussistente tra l'energia media e la temperatura del sistema.
Specifichiamo che ogni dipendenza quadratica del sistema viene chiamata grado di libertà quadratico oppure "modo" del sistema.
La molla dell'esempio di poco fa possiede dunque 2 gradi di libertà quadratici.
Nell'esempio generico appena illustrato abbiamo invece constatato come ogni grado di libertà del sistema vada a contribuire per un ammontare di energia pari a 1/2 kBT all'energia totale media del sistema.
Questo ragionamento sta alla base del teorema di equipartizione dell'energia:
"Se l'energia di un sistema classico è la somma di n gradi di libertà quadratici, e quel sistema è in contatto con un serbatoio termico a temperatura T, allora l'energia media del sistema viene fornita da

"
Il teorema di equipartizione rende palese il fatto che l'energia risulta "suddivisa egualmente" tra tutti i modi separati del sistema, ciascuno avente energia media pari a precisamente 1/2 kBT.
Vediamo un facile esempio di applicazione del teorema.
Consideriamo un gas monoatomico.
Essendo monoatomico, nel moto di ciascun atomo del gas non sussistono componenti rotazionali o vibrazionali, ma solamente traslazionali.
Questo significa che è possibile esprimere l'energia di ciascun atomo come:

dove il vettore

designa la velocità dell'atomo.
Tale energia è la somma di 3 gradi di libertà quadratici indipendenti, e pertanto il teorema di equipartizione restituisce la seguente energia media:

Senza entrare nei dettagli tecnici, diciamo solo che se avessimo considerato un gas biatomico, in cui è possibile avere dei termini aggiuntivi di energia cinetica rotazione e vibrazionale, il teorema di equipartizione ci avrebbe restituito un'energia media pari a

o addirittura

Ergo, in generale, l'energia media viene fornita dalla relazione:

dove f è il numero dei gradi di libertà quadratici.
Giungiamo ora al nocciolo della questione: il moto browniano.