SCATTERING RAYLEIGH E SCATTERING THOMSON

In fisica un fenomeno assai rilevante è quello della diffusione o dispersione ottica, spesso indicata col termine inglese scattering, letteralmente "sparpagliamento".
Trattasi sostanzialmente di quel fenomeno (o meglio, ampia classe di fenomeni) per cui onde o particelle vengono deflesse per via delle collisioni con altre onde o particelle.
Esiste un variegato numero di fenomeni di scattering notevoli.
In passato abbiamo visto brevemente per esempio lo scattering Compton (o effetto Compton) qui.
In questo post presenteremo in modo (per quanto possibile) semplice e sintetico 2 tipi di scattering anch'essi molto importanti: lo scattering Rayleigh e lo scattering Thomson.
Prima di far ciò dobbiamo tuttavia compiere qualche premessa.
Innanzitutto ci serve capire l'importante concetto di sezione d'urto.
Immaginiamo a tal proposito di sparare un fascio di particelle su un certo campione di materiale e di voler studiare l'interazione sussistente.
Denotiamo con $N(x)$ il numero di particelle del fascio incidente (proiettili) che incidono nell’unità di tempo sulla unità di superficie del campione lungo l’asse $x$.
Indichiamo poi con $\Delta x$ un piccolo spessore del campione.

 

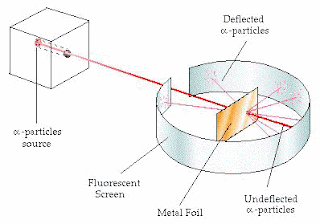
Per capire meglio, prendiamo a riferimento l'esperimento di Rutherford (di cui abbiamo accennato qui).

 

Sappiamo da esso che il numero di particelle diminuisce una volta urtato il materiale, giacché alcune particelle vengono deviate e non riescono a giungere all'analizzatore.
Nel nostro contesto generale ciò significa che

Notiamo immediatamente che

Inoltre il rapporto $\Delta N/N$ risulterà proporzionale allo spessore $\Delta x$ attraversato.
Nel dettaglio:

Qui $\eta$ è una costante maggiore di 0 che rappresenta la probabilità di deviazione delle particelle. Il segno - mette in evidenza la diminuzione dei proiettili nell’attraversamento dello spessore $\Delta x$.
Per giungere alla formula appena scritta si è assunta un’ipotesi semplificativa nota come condizione di urto singolo.
Si assume infatti che lo spessore del campione in esame sia così sottile che dopo il primo urto tra proiettile e bersaglio non ce ne siano altri.

Si assume inoltre che i bersagli nel campione siano abbastanza lontani gli uni dagli altri in modo che ciascun proiettile ne intercetti uno solo.
Va specificato che la costante $\eta$ dipende dal numero dei centri diffusori (bersagli) nell’unità di volume (cioè in pratica dalla loro densità).
Possiamo infatti scrivere anche che

 

ove $n = \frac{N_{BERS}}{V}$ è appunto la densità dei bersagli, mentre la grandezza $\sigma$ è la sezione d'urto totale del processo.

Siamo riusciti dunque a introdurre matematicamente questo importante concetto di sezione d'urto, ma cosa rappresenta concretamente?
Essa rappresenta semplicemente la probabilità, per singolo bersaglio, che ci sia l'interazione tra il proiettile e il bersaglio e ha le dimensioni fisiche di un'area!
Infatti si può scrivere:

 

Detto in altri termini, la sezione d'urto può essere interpretata come l'area efficace per la diffusione.

Ogni bersaglio espone al flusso di particelle incidenti un'area (sferica) $\sigma$ e soltanto le particelle che intercettano quest'area vengono deviate.

La seguente immagine, tratta dal libro Particles and Nuclei: An Introduction to the Physical Concepts di B. Pohv, K. Rith, C. Scholz, F. Zetsche e W. Rodejohann, dovrebbe ben chiarire il concetto.

 

Si potrebbe poi facilmente dimostrare che il numero di particelle $N(x)$, a seguito della penetrazione in uno spessore $x$, decresce in modo esponenziale con una costante di decadimento $n \sigma$. In simboli:

Inoltre, se andassimo nel dettaglio dello scattering Rutherford, dovremmo introdurre il concetto di sezione d'urto differenziale $\frac{\mathrm{d} \sigma}{\mathrm{d} \Omega}$, ove $\mathrm{d} \Omega$ denota un angolo solido (infinitesimo) intorno ad una certa direzione, il quale tiene conto dell'importante distribuzione angolare delle particelle deflesse.
Questo discorso esula però dagli scopi del presente post; magari torneremo sulla questione in futuro.
Abbiamo dunque capito in un contesto piuttosto generale cosa sia la sezione d'urto.
Il prossimo importante step del nostro discorso è ricordare che l'elettrodinamica classica stabilisce che una particella carica (non relativistica) emette radiazione elettromagnetica quando subisce una variazione di velocità (ossia un'accelerazione); la potenza della radiazione così emessa viene descritta dalla nota formula di Larmor:

Per maggiori dettagli si rilegga qui.

Nel contesto dello scattering Rayleigh e di quello Thomson si potrà parlare di una sezione d'urto dipendente dalla frequenza della radiazione incidente. 

In particolare, la sezione d'urto $\sigma(\omega)$ va a rappresentare l'efficienza di emissione di radiazione da parte di un atomo, in funzione della frequenza incidente $\omega$.

Essa è strettamente legata alla potenza di Larmor dalla relazione

dove $I_0$ è l'intensità incidente e la notazione $<P_{\mathrm{Larmor}}>$ serve per denotare la potenza media. 
Specifichiamo che l'intensità di un'onda elettromagnetica rappresenta l'energia che attraversa la superficie ortogonale alla velocità di propagazione dell'onda, nell'unità di tempo.

Nello specifico, essa corrisponde al modulo del fondamentale vettore di Poynting, ma non entriamo nei dettagli di tale discorso.

Grazie alla formula di Larmor, assumendo poi il cosiddetto modello di Thomson, ove immaginiamo l'elettrone alla stregua di un oscillatore armonico smorzato con forzante esterna (per capire meglio si rilegga magari qui), con un po' di passaggi matematici si arriva a scrivere che

Qui $X$ è un modo sintetico per denotare la quantità $\sqrt{(\omega_0^2 - \omega^2)^2 + \gamma^2 \omega^2}$, in cui $\omega_0$ è la pulsazione propria del sistema e $\gamma$ è il coefficiente di smorzamento. Inoltre $e$ è la carica dell'elettrone, $m$ la sua massa, $\varepsilon_0$ la costante dielettrica del vuoto e $c$ la velocità della luce.

Definiamo ora il raggio classico dell'elettrone $r_e$ come

Esso si ottiene molto facilmente uguagliando l'energia elettrostatica di una sfera di carica $e$, avente raggio $r_e$, cioè $U = \frac{1}{4 \pi \varepsilon_0} \frac{e^2}{r_e}$, con l'energia a riposo $mc^2$ dell'elettrone.

Per convenienza, scriviamo pure che

Manipolando un pochino l'espressione precedente data per $<P_{\mathrm{Larmor}}>$ e tenendo presente il valore delle quantità prima riportate, possiamo in definitiva scrivere

da cui è facile ricavare che

Trattasi dell'espressione generale della sezione d'urto di diffusione (incoerente).

A questo punto andiamo ad osservare cosa succede in 3 casi limite.