DERIVATE E INTEGRALI INDEFINITI: STORIA, PROPRIETÀ E APPLICAZIONI IN FISICA

Le derivate e gli integrali indefiniti sono 2 concetti chiave dell'analisi matematica, che trovano moltissime applicazioni in fisica.
Cominciamo introducendo cos'è la derivata: in termini semplici, la derivata è il coefficiente angolare della retta tangente a una curva (una funzione) che prendiamo in considerazione, in un punto specifico.
L'immagine seguente illustra il concetto graficamente: le immagini, molto spesso, sono più significative delle parole!



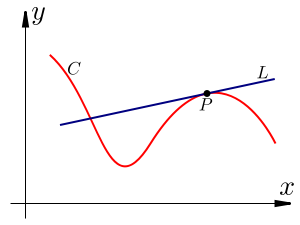
La retta L tangente in P alla funzione f ha pendenza data dalla derivata di f in P.
La definizione più precisa richiede l'utilizzo di un altro concetto fondamentale dell'analisi matematica: il limite.
Illustriamo brevemente il concetto di limite (molto semplificato) attraverso un esempio: se noi abbiamo una funzione f(x), per esempio y = (x+5)/x, se volessimo calcolare il limite quando x tende a -1, dovremmo andare a sostituire il -1 all'equazione sopracitata: otterremmo 4/-1 = -4: dunque il limite della funzione considerata è -4.
Pertanto il limite di una funzione, ci indica il valore cui tende la funzione considerata quando x tende a un valore, che può essere un numero reale qualsiasi, oppure infinito.
Prima di concludere la descrizione della definizione di derivata, occorre introdurre un altro concetto: il rapporto incrementale.
Data una funzione y = f(x), consideriamo una sua ascissa x = c e il corrispondente valore della funzione f(c).
Dopodiché prendiamo in considerazione l'ascissa x = c + h, ottenuta incrementando il valore di c di una quantità h, e il corrispondente valore della funzione, ossia f(c+h).
Osserviamo che a un incremento delle ascisse Δx = h corrisponde un incremento delle ordinate Δy = f(c+h) - f(c), che rappresenta l'incremento della funzione quando x passa dal valore c al valore c + h.
Il rapporto incrementale è dunque questo:






Una volta definito il rapporto incrementale, la definizione di derivata è molto semplice: non è altro che il limite del rapporto incrementale, quando l'incremento h tende a 0.
In simboli:



La derivata di una funzione può essere indicata con varie notazioni:

- f'(x)
- y'
- dy/dx: questa è la notazione di Leibniz introdotta nel suo articolo del 1684 dal titolo Nova methodus pro maximis et minimis, itemque tangentibus, qua nec irrationales quantitates moratur.
- Df(x)

Proviamo a calcolare, basandoci sulla definizione, una semplicissima derivata di una funzione: la derivata di y = 3x² - 2x.
Calcoliamo, in primo luogo, il rapporto incrementale: consideriamo la funzione y = 3x² - 2x e la funzione (con l'aggiunta dell'incremento) y = 3(x+h)² - 2(x+h).
Il rapporto incrementale si ottiene così:

Δy/Δx = (3(x+h)² - 2(x+h) - (3x² - 2x))/h.
(3(x² + h² + 2xh) - (2x + h) - 3x² + 2x)/h.
(3x² + 3h² + 6xh - 2x - 2h - 3x² + 2x)/h.
Semplificando: (3h² + 6xh - 2h)/h.
Raccogliendo la h: h(3h + 6x - 2)/h
Si ottiene pertanto: 3h + 6x - 2.
Adesso, calcolando il limite del rapporto incrementale per h che tende a 0: otteniamo 6x - 2: ecco la derivata della funzione!
Questo esercizio poteva essere risolto molto più semplicemente e velocemente facendo ricorso ad alcune regole inerenti il calcolo delle derivate.
In particolare:
Applicando tale regola fondamentale all'esercizio precedente, esso si risolve immediatamente, senza ricorrere a limiti e rapporti incrementali.
Ecco una tabella contenente alcune delle derivate fondamentali:



Andiamo a vedere alcune applicazioni delle derivate in fisica.
La prima che analizziamo riguarda la meccanica classica: consideriamo la legge oraria del moto, ossia la funzione s = s(t) che esprime lo spazio percorso da un corpo al variare del tempo.
Si può definire poi la nota grandezza della velocità media, come Vm = Δs/Δt, cioè spazio percorso diviso tempo impiegato a percorrerlo.
La velocità media assume perciò il ruolo di rapporto incrementale della funzione s = s(t).
Ma sussiste un'altra tipologia ben nota di velocità, la velocità istantanea, ossia quella che un corpo possiede in uno specifico istante.
Essa è il limite della velocità media quando l'intervallo di tempo Δt tende a 0.
Ma la derivata non è il limite del rapporto incrementale quando l'incremento h tende a 0?
Dunque, traslando la definizione di derivata, in questo contesto fisico, possiamo dire che la velocità istantanea non è altro che la derivata dello spazio rispetto al tempo:

v(t) = s'(t)

Proviamo, per esempio, a ricavare da questa formula s(t) = 1/2 at² + V0t + S0, che rappresenta la legge oraria del moto uniformemente accelerato (in cui l'accelerazione a è costante), la velocità istantanea, attraverso il processo di derivazione.
Prima di ciò, specifichiamo che:

-V0 = velocità iniziale;
-S0 = spazio iniziale.

Deriviamo allora tale funzione: otteniamo che 1/2 at² diventa at; V0t diventa V0, mentre S0 scompare.
Alla fine abbiamo che v(t) = V0 + at, che è proprio la formula della velocità istantanea del moto rettilineo uniformemente accelerato. CVD!
Ulteriore notizia: se noi derivassimo per la seconda volta la funzione data, ossia staremmo calcolando la cossidetta derivata seconda, si guardi cosa si ottiene:

Prendiamo v(t) = V0 + at, che è la derivata prima della funzione iniziale; adesso deriviamo ancora, ossia calcoliamo la derivata seconda: il termine V0 scompare, mentre di at rimane solamente a.
Dunque otteniamo la relazione a(t) = a, ossia che l'accelerazione in funzione del tempo è l'accelerazione stessa: cioè a è costante, condizione che avevamo posto inizialmente e che adesso abbiamo verificato.
Inoltre, da questa dimostrazione, si capisce che l'accelerazione istantanea è la derivata prima della velocità istantanea ed è pure la derivata seconda dello spazio rispetto al tempo.
In simboli:

aist = v'(t) = s''(t)

Si percepisce da questi esempi che le derivate ci permettono di ricavare le note formule della fisica che si imparano (spesso) a memoria a scuola: rappresentano, per questo motivo, uno strumento più potente ed efficace per la fisica rispetto agli strumenti dell'algebra classica.
Facciamo un altro esempio di applicazione della derivata in fisica: proviamo a ricavare la nota legge di Hooke sulla forza elastica di una molla.
Prima di tutto è necessario affermare che, quando un corpo si muove lungo una linea retta sotto l'azione di una forza conservativa, l'energia potenziale U è una funzione della sua posizione x e la derivata di tale funzione, cambiata di segno, è uguale alla forza che agisce sul corpo.
Quindi vale tale relazione: F(x) = -U'(x).
Se consideriamo adesso una molla fissata ad una parete, assumiamo come asse x quello della direzione dell'allungamento e consideriamo come origine l'estremo libero della molla nella sua posizione di riposo, si ottiene allora una situazione in cui vale la legge sopracitata.
Siccome l'energia potenziale elastica di una molla deformata con uno spostamento x, è definita in questo modo: U(x) = 1/2 kx², dove k = costante elastica della molla, allora derivando quest'ultima relazione otteniamo:

F(x) = -U'(x) = -kx, che non è altro che la famosa legge di Hooke. CVD!

Abbiamo osservato le proprietà della derivata e la sua importanza in fisica: adesso occupiamoci di un altro importantissimo concetto dell'analisi matematica: l'integrale indefinito.
Bisogna dire che la comprensione di tale strumento, quando si è riusciti a capire cos'è la derivata, viene da sé: infatti derivata e integrale indefinito non sono altro che l'uno l'inverso dell'altro.
Per capire ciò, consideriamo per esempio la funzione y = 2x, che ha derivata y' = 2; adesso consideriamo la funzione y = 2x + 1, che ha derivata y' = 2; consideriamo la funzione y = 2x + 2, che avrà sempre derivata y' = 2.
Notiamo che diverse (anzi infinite) funzioni possiedono sempre la stessa derivata.
Per provarlo nuovamente, basta cambiare la funzione di partenza: y = 3x² ha derivata y' = 6x; y = 3x² + 1 ha derivata sempre y' = 6x e così via.
Le funzioni che danno origini a singole derivate sono dette primitive o antiderivate.
Dettò ciò, l'integrale indefinito è uno strumento che serve, partendo da una funzione derivata qualsiasi, a risalire alle sue infinite primitive.
Prendiamo ad esempio la semplicissima funzione y = x, la cui derivata è y' = 1.
Adesso intraprendiamo il processo inverso: consideriamo y' = 1: come facciamo a risalire alla funzione di partenza (ossia alla famiglia di primitive)?
The answer is: utilizziamo il processo di integrazione!
Possiamo scrivere il tutto in questo modo: ∫(1) dx = x + c.
Altro esempio: data la derivata y' = 2x, l'integrale indefinito è: ∫2x dx = x² + c.
In generale si definisce integrale indefinito di una funzione derivata f(x) l'insieme di tutte e sole le funzioni primitive di f(x).
In simboli:

∫f(x) dx = F(x) + c, dove F'(x) = f(x) con c ∈ R

Quel parametro c che compare non è altro che una costante.
Infatti, se F(x) è una primitiva di f(x), allora anche F(x) + c è una primitiva di f(x) in quanto, come sappiamo, la derivata di una costante è nulla.
Perciò una funzione che ammette una primitiva, ammette infinite primitive e distinte.
Ritornando propriamente all'integrale indefinito, specifichiamo che la scrittura ∫f(x) dx si legge: integrale indefinito di f(x) in dx.
Inoltre, la funzione f(x) che rappresenta una derivata, in questo contesto viene chiamata funzione integranda, mentre la variabile x è detta variabile di integrazione.
Anche per quanto riguarda gli integrali indefiniti ne esistono alcuni fondamentali, riportati qui sotto:



Proviamo giusto a ritrovare l'insieme delle primitive di una semplice funzione: y' = 3sen x:

∫3senx dx = -3cosx + c, in quanto, come riportato sopra, l'integrale indefinito di sen x = - cos x.

Per quanto riguarda le applicazioni alla fisica degli integrali indefiniti, facciamo riferimento alle grandezze fondamentali del moto (spazio, tempo, velocità, accelerazione) e vediamo cosa succede.
Avevamo detto che la velocità istantanea di un corpo è la derivata rispetto al tempo della funzione s(t), che esprime la legge del moto: v(t) = s'(t).
Avevamo anche detto che l'accelerazione istantanea è la derivata della velocità: a(t) = v'(t).
Adesso, conoscendo lo strumento dell'integrale indefinito, possiamo constatare che:

- la legge oraria del moto è una primitiva della velocità, cioè: s(t) = ∫v(t) dt;
- la velocità è una primitiva dell'accelerazione, ossia: v(t) = ∫a(t) dt.

Pertanto, tutte queste leggi riguardanti il moto possono essere espresse in maniera chiara e significativa sfruttando i concetti di derivata e integrale indefinito.
Bene: adesso che abbiamo ultimato questa breve trattazione di alcune proprietà e delle applicazioni fondamentali di tali strumenti matematici in fisica, possiamo introdurre un po' di storia dell'analisi matematica, in cui spicca la celebre disputa tra Newton e Liebniz.

BREVE STORIA DELLE ORIGINI DELL'ANALISI MATEMATICA

Verso la fine del XVII secolo 2 grandissimi scienziati, il tedesco Gottfried Wilhelm Leibniz (1646-1717) e l'inglese Isaac Newton (1642-1727), si contesero il primato di chi avesse dato origine all'analisi infinitesimale.
In realtà, le vere origini di questa importantissima branca della matematica sono molto più antiche: i ragionamenti di Zenone d'Elea (molto celebre per il paradosso di Achille e la tartaruga), le dimostrazioni di Eudosso, i calcoli di Archimede e, successivamente, i lavori di Cavalieri, Galilei, Torricelli, Pascal e Fermat, furono assolutamente determinanti per innestare le condizioni necessarie allo sviluppo di questa nuova disciplina, che inizialmente, prese la denominazione di Calcolo sublime.
Newton aveva introdotto il metodo delle flussioni per risolvere questioni di natura fisica, come il problema della velocità istantanea, mentre Liebniz aveva utilizzato il metodo delle differenze infinitesime per risolvere questioni specificamente matematiche, come il problema della tangente a una curva.
L'inglese aveva scritto (senza però pubblicarli) ben 3 scritti nei quali tentava di giustificare il suo calcolo infinitesimale:

- nel primo (De analysi per aequationes numero terminorum infinitas), del 1669, ammetteva esplicitamente che il suo metodo era "spiegato brevemente piuttosto che dimostrato";
- nel secondo (Methodus fluxionum et serierum infinitarum), risalente al 1671, parlava di grandezze che potevano variare con continuità e assumere valori anche non discreti (usava il termine tecnico "flussione");
- nel terzo (De quadratura curvarum), pubblicato nel 1704, cercava di fornire una spiegazione più precisa e soddisfacente di cosa intendesse per flussione, ma non ci riuscì pienamente.

Infatti, Newton chiarì in maniera migliore la sua concezione di calcolo infinitesimale parlando di fisica nel suo capolavoro Philosophiae naturalis principia mathematica (1687).
Dall'altro lato, Liebniz, aveva pubblicato il suo primo studio sul calcolo infinitesimale negli Acta eruditorum del 1684 e impostato il suo lavoro in maniera completamente originale: parlava di valori che erano "infinitamente piccoli", non pari a 0, ma comunque più piccoli di qualunque numero dato.
Il tedesco prendeva in considerazione 2 punti appartenenti a una curva e affermava che, se essi erano "infinitamente vicini", allora dx era la differenza tra le loro ascisse e dy la differenza fra le loro ordinate.
Liebniz, così come Newton, non riuscì tuttavia a spiegare il suo metodo di calcolo in maniera soddisfacente, tanto che i suoi amici, leggendo il suo primo scritto, commentarono: "Un enigma più che una spiegazione".
Dunque, in questa prima fase, i 2 scienziati si scambiarono lettere e segnali di reciproca stima.
La situazione cambiò profondamente quando, nel 1695, Newton venne a conoscenza che in Europa si attribuiva il merito dell'invenzione del calcolo differenziale a Liebniz: da quel momento in poi i rapporti tra i 2 scienziati si interruppero violentemente.
È necessario specificare che certamente il lavoro di Newton era antecedente a quello di Liebniz, tuttavia l'inglese, come detto in precedenza, non pubblicò nulla.
I risultati di Leibniz, al contrario, non solo furono pubblicati tempestivamente, ma visto che sono stati ottenuti mediante un approccio più geometrico e per molti versi più naturale, fecero rapidamente presa in Europa.
In effetti, ancora oggi, l'approccio alla differenziazione di Leibniz, ossia un approccio geometrico, è quello generalmente adottato nei corsi di calcolo infinitesimale in tutto il mondo e la notazione da egli utilizzata per la derivata è usata spesso anche oggi, mentre la notazione e l'approccio in termini di moto fisico preferiti da Newton, vengono di rado utilizzati al di fuori della fisica.
Si instaurò così una scottante questione, che mutò in aspra polemica: Liebniz era arrivato ad introdurre l'analisi infinitesimale autonomamente, oppure, aveva saputo del nuovo calcolo che Newton stava sviluppando e quindi aveva copiato?
Sussistevano elementi a favore di questa seconda tesi: i 2 scienziati si erano scambiati, nella prima fase, diversi commenti sull'argomento, e ad avvalorare tale ipotesi concorreva il fatto che Liebniz aveva soggiornato a Londra nel 1673, e pertanto era sicuramente entrato in contatto con i lavori di Newton.
Vennero lanciate durissime accuse nei confronti del tedesco.
Su insistenza dello stesso Leibniz, la Royal Society nominò una commissione d'inchiesta per dirimere la questione: l'esito finale (nel 1712) diede ragione a Newton: Liebniz fu accusato di spudorato plagio.
Con ogni probabilità, Newton, in qualità di presidente della Royal Society, non fu estraneo al verdetto della commissione.
Liebniz respinse sempre le aspre accuse imputategli, rivendicando con fermeza l'autonomia delle proprie ricerche, anche se non mise mai in discussione il fatto che Newton avesse inventato per primo l'analisi infinitesimale.
La polemica continuò persino dopo la morte di Leibniz, comportando come conseguenza l'interruzione, per diversi decenni, dello scambio scientifico tra la scuola inglese e quella continentale.
Oggi non ha senso parlare del "vero padre" del calcolo infinitesimale: entrambi diedero contributi fondamentali, che vennero ripresi e implementati dagli analisti successivi.
Inoltre, bisogna osservare che in queste prime formulazioni del calcolo, e in generale per tutto il Settecento, era la derivazione ad esser considerata l'operazione principale, mentre l'integrazione non era vista come un'operazione indipendente, bensì solo come l'inversa della derivazione.
Il posto in secondo piano assunto dall'integrazione durò ben poco, visto che Augustin Louis Cauchy e George Bernard Riemann svilupparono il concetto di integrale definito (indipendente dalla derivazione), importantissimo per calcolare lunghezze, aree e volumi.
Un'ulteriore significativa generalizzazione della teoria dell'integrazione venne da Henry Lebesgue, il quale nel 1902 propose una nuova definizione di integrale, la quale può essere considerata l'estensione della definizione di integrale fornita da Riemann.
Da questo momento, l'integrazione assunse la stessa importanza della derivazione, se non superiore.

P.S.

Dato che siamo in periodo natalizio, pubblico alcuni video inerenti stupende interpretazioni di musiche (anche la musica è matematica!) di Natale:

1) Barbra Streisand in Jingle Bells:



2) Celine Dion in Blue Christmas:



3) Carmen Cavallaro in White Christmas:



4) Renee Olstead in Christmas in Love:



5) Andre Rieu in Silent Night:



6) Kenny G in Have Yourself a Merry Little Christmas:



7) Ryuichi Sakamoto in Merry Christmas Mr. Lawrence:



8) Ella Fiztgerald in Santa Claus is coming to Town:



In più: un video di ripasso delle derivate fondamentali come sorpresa finale!

CFC, BUCO NELL'OZONO, EFFETTO SERRA: DIVAGAZIONI SU FISICA E CHIMICA

Le relazioni che intercorrono tra fisica e chimica sono innumerevoli: si può affermare che queste 2 discipline rappresentino le basi su cui poggia l'intera scienza moderna, espressa poi con il linguaggio universale della matematica.

In tale contesto, andremo ad analizzare i rapporti tra fisica e chimica inerenti l'ambiente e l'atmosfera terrestre, studiati principalmente dalle scienze dell'atmosfera.
Partiamo, a questo punto, da un gruppo di sostanze chimiche che hanno comportato notevoli effetti nocivi proprio a scapito della nostra atmosfera: i CFC.

CFC (CLOROFLUOROCARBURI)

I CFC (clorofluorocarburi) sono sostanze divenute famose, in quanto a esse viene imputata la causa del cosidetto "buco nell'ozono".
Prima di trattare in maniera specifica gli effetti negativi dei CFC, dobbiamo soffermarci sul ruolo assunto da tali composti, fin quando non si svelò il loro "lato oscuro".
Furono introdotti negli anni '30 del XX secolo dall'ingegnere meccanico Thomas Midgley jr. e dal chimico Albert Henne come sostanze refrigeranti ideali.
La molecola refrigerante perfetta deve possedere alcuni requisiti fondamentali:

1) deve passare allo stato gassoso nel giusto intervallo di temperature;
2) deve liquefarsi (liquefazione = passaggio dallo stato aeriforme a quello liquido) per compressione, sempre all'interno dell'intervallo di temperature richiesto;
3) infine, deve assorbire quantità di calore relativamente grandi nel momento in cui passa allo stato di vapore.

Alcune sostanze, tra cui l'ammoniaca, l'etere, il cloruro di metile, il diossido di zolfo, ecc., rispondevano a questi prerequisiti che dovevano avere le sostanze per essere considerate buoni refrigeranti.
Purtroppo, tali composti possedevano aspetti negativi, come il fatto di decomporsi, oppure di essere infiammabili, velenosi o maleodoranti, o a volte anche più di uno.
Proprio per cercare di ridurre i rischi di tossicità e di esplosioni, i 2 scienziati sopracitati cominciarono a esaminare vari composti, con la speranza di trovarne alcuni con punti di ebollizione all'interno dell'ambito definito del ciclo di refrigerazione.
Tuttavia, la maggior parte delle sostanze che soddisfacevano tale richiesta erano già in uso, oppure era state scartate, in quanto poco pratiche.
Ma rimaneva una speranza: non erano ancora stati presi in considerazione i composti del fluoro.
Il fluoro, preso come singolo elemento, è un gas altamente tossico e corrosivo.
Inoltre, fino ad allora, erano stati preparati pochissimi composti organici contenenti fluoro.
Midgley e Henne elaborarono così un certa quantità di molecole diverse, contenenti 1 o 2 atomi di carbonio e un numero variabile di atomi di fluoro e cloro, in sostituzione degli atomi di idrogeno.
Si ottennero in questo modo i clorofluorocarburi (CFC), i quali rispondevano in maniera esemplare ai vari prerequisiti sopraelencati ed erano, inoltre, anche molto stabili, non infiammabili, non tossici, poco costosi per l'azienda produttrice e quasi inodori.
Addirittura Midgley, durante un convegno dell'American Chemical Society ad Atlanta (Georgia), per dimostrare il loro carattere del tutto innocuo, si sottopose ad un esperimento molto singolare: versò un po' di CFC liquido in un recipiente aperto e, mentre il refrigerante bolliva, avvicinò il viso al vapore, aprì la bocca e aspirò profondamente.
Dopodiché si voltò verso una candela accessa ed esalò lentamente i CFC, spegnendo in questo modo la fiamma: è sicuramente una dimostrazione esemplare del fatto che tali sostanze non sono assolutamente tossiche, tantomeno esplosive.
Da allora, varie molecole di CFC furono utilizzate come refrigeranti, tra cui:

- il diclorodifluorometano (Freon 12);
- il triclorotrifluorometano (Freon 11);
- l'1,2-dicloro-1,1,2,2-tetrafluoroetano (Freon 114).



Freon-114


L'entusiasmo nei confronti dei CFC iniziò a vacillare a partire dal 1974, quando i ricercatori Sherwood Rowland e Mario Molina annunciarono risultati preoccupanti.
I 2 scienziati avevano trovato che la stessa stabilità tanto apprezzata dei CFC comportava un problema del tutto inatteso ed estremamente allarmante.
Diversamente da composti meno stabili, i clorofluorocarburi non vengono scomposti da comuni reazioni chimiche.
Proprio a causa di ciò, i CFC liberati nell'atmosfera inferiore (troposfera) vi vagano per anni o addirittura decenni, fino a quando non salgono nella stratosfera, in cui vengono scomposti dalla radiazione solare.
Proprio nella stratosfera c'è uno strato di ozono (ozonosfera) che si estende da 15 a 30 km circa al di sopra della superficie terrestre.
L'ozono è una forma particolare di ossigeno composta, non come avviene solitamente, da 2 atomi di tale elemento (O2) bensì da 3 (O3).
Le 2 molecole in questione possiedono proprietà ben diverse.
Al di sopra dell'ozonosfera, l'intensa radiazione solare rompe il legame sussistente tra i 2 atomi in una molecola di ossigeno, producendo così 2 atomi di ossigeno indipendenti.
Questi ultimi ridiscendono nello strato d'ozono, nel quale ognuno di loro reagisce con un'altra molecola di ossigeno, formando una molecola di ozono.
Poi, all'interno dell'ozonosfera, le molecole (di ozono) vengono scomposte dalla radiazione UV ad alta energia, generando una molecola di ossigeno e un atomo di ossigeno.
Dopodiché 2 atomi di ossigeno si ricombinano formando la molecola O2.
In questo modo, nello strato di ozono, quest'ultimo viene costantemente prodotto e scomposto.
Nel corso dei millenni si è raggiunta una situazione di equilibrio: dunque la concentrazione di ozono nell'atmosfera terrestre rimane per lo più costante.
Tale fatto comporta conseguenze importanti per la vita sulla Terra: l'ozonosfera assorbe la parte della radiazione UV solare più dannosa per gli organismi viventi, funzionando alla stregua di un ombrello sotto cui noi ci ripariamo.
Dettò ciò, le ricerche di Rowland e Molina hanno dimostrato che gli atomi di cloro incrementavano il tasso di decomposizione delle molecole di O3.
Si veniva così a inceppare quell'equilibrio tra molecole di ozono e molecole di ossigeno, in quanto gli atomi di cloro rendono più rapida la scomposizione di O3, ma non hanno alcun effetto sulla sua produzione.
L'aspetto più allarmante di questo fenomeno sta nel fatto che non solo le molecole di ozono sono distrutte dal cloro, ma addirittura quest'ultimo agisce da catalizzatore, ossia aumenta il ritmo della reazione senza consumarsi.
Si stima che ogni atomi di cloro che riesca a giungere nell'atmosfera superiore mediante una molecola di CFC, prima di essere disattivato, distruggerà centinaia di migliaia di molecole di ozono!
Inoltre, per ogni 1% di diminuzione dello strato di O3, potrebbe penetrare nell'atmosfera terrestre un 2% addizionale della dannosa radiazione ultravioletta.
Dettò questo, il lato oscuro dei CFC si mostrò in maniera evidente con il celebre "buco nell'ozono".
Infatti, studi compiuti nel 1985 mostrarono che lo strato d'ozono presente al di sopra dell'Antartide si stava "svuotando", generando un gigantesco "buco".
Tutto ciò diede una dimostrazione del fatto che le conseguenze dei CFC erano globali, visto che nel Polo Sud, essendo una zona per lo più disabitata, non c'era una grande richiesta di frigoriferi o di lacche spray per capelli (dunque era veramente esiguo l'utilizzo di CFC).
La scoperta mise in allerta la comunità scientifica internazionale.
Nel 1987 fu approvato il Protocollo di Montreal (aggiornato nel 1990 e nel 1992), in seguito al quale l'impiego su scala mondiale dei più nocivi CFC diminuì del 40% in 5 anni.
Ciò nonostante, a partire dal 1994, l'onozo stratosferico al di sopra dell'Antartide risultava ormai completamente distrutto.
Oggi si usano come refrigerenti, al posto dei clorofluorocarburi, gli idrofluorocarburi e gli idrofluoroclorocarburi.
Tali sostanze, da una parte non danno vita agli effetti nocivi generati dai CFC, ma dall'altra non sono altrettanto efficaci come refrigeranti, e richiedono un 3% aggiuntivo di energia per il ciclo di refrigerazione.
Nell'atmosfera, comunque, vi sono ancora miliardi di molecole di CFC e inoltre, non tutti i paesi hanno firmato il Protocollo di Montreal.
Ad aggravare la situazione concorre il fatto che persino nei Paesi che lo hanno firmato, sono ancora in uso milioni di frigoriferi che li contengono.
Riassumendo, ci troviamo pertanto di fronte a delle molecole che per qualche decennio sono state giudicate in maniera assolutamente positiva, ma che, a partire dagli anni 70', sono divenute un vero e proprio problema globale: esse potrebbero continuare a fare danni per secoli.
Specifichiamo che la quantità di ozono nell'atmosfera si misura in Dobson (DU), unità di misura che prende il nome da Gordon Miller Bourne Dobson, uno dei primissimi studiosi dell'ozono atmosferico, che aveva progettato anche un particolare strumento per misurare l'O3, lo spettrometro Dobson.
Molto spesso si è soliti collegare il buco nell'ozono ad un altro celebre fenomeno: l'effetto serra.
È necessario affermare che un vero e proprio rapporto stretto di causa-effetto tra di essi non c'è.
Tuttavia, sussistono legami indiretti, primo fra tutti il fatto che i CFC, oltre a provocare il buco nell'ozono, sono anche gas serra, ossia vanno ad incrementare e potenziare l'effetto serra.

EFFETTO SERRA

Prima di tutto, specifichiamo che in assenza dell'effetto serra non potremmo vivere.

Questa sembrerà un'affermazione scellerata agli occhi di coloro che quando sentono nominare il termine "effetto serra", subito gli assegnano una connotazione del tutto negativa.
Non è così: tale effetto riscalda la superficie del nostro pianeta, mantenendo così una temperatura che permette la nascita e lo sviluppo della vita.
Se non ci fosse l'effetto serra, la Terra sarebbe una grande palla (se vogliamo essere puntigliosi un "geoide") gelata.
Essa sarebbe infatti circa 30 gradi più fredda, con una temperatura media del globo di -18 °C (l'acqua, la molecola basilare della vita, allo stato liquido sarebbe sostituita dal ghiaccio: fatto problematico allo sviluppo della vita stessa).

Dunque dobbiamo ringraziare l'effetto serra: thank you very much!!
Il "lato oscuro di questo fenomeno" esce quando ci si intromette l'uomo.
Ma prima di arrivare a tutto questo, andiamo ad analizzare come funziona l'effetto serra.
L'atmosfera riduce la quantità di radiazione solare che raggiunge il suolo terrestre.
Le nubi riflettono circa il 30% della luce solare che le colpisce e assorbono il 15% di quella che le attraversa.
Un'atmosfera limpida e senza nuvole riesce ad assorbire soltanto il 17% della luce solare che la attraversa.
Anche il suolo terrestre fa la sua parte: la neve fresca riflette fino al 90% della radiazione solare, la sabbia dei deserti il 30% circa, mentre oceani e foresti pluviali ne assorbono oltre il 90%.
In generale la superficie terrestre assorbe una parte della radiazione solare e poi la riemette sotto forma di radiazione infrarossa.
L'atmosfera è costituita principalmente da azoto (78%) e ossigeno (21%), i quali risultano pressocché trasparenti alla radiazione termica infrarossa, e la lasciano sfuggire verso lo spazio.
Ma (adesso arriva il punto cruciale) esistono alcune tipologie di gas che assorbono e rimandano la radiazione infrarossa verso la terra: ecco l'effetto serra.
Quindi, come abbiamo detto, l'effetto serra riscalda il nostro pianeta e permette la vita: il problema però si crea quando l'uomo ci mette lo zampino!
Intanto, possiamo stilare una lista dei fondamentali gas serra:

1) anidride carbonica o diossido di carbonio (CO2);
2) vapore acqueo;
3) metano;
4) ossido di azoto;
5) CFC;
6) idroclorofluorocarburi (HCFC);
7) idrofluorocarburi (HFC), ecc.

La combustione di petrolio e carbone da parte dell'uomo concorre ad incrementare la concentrazione di gas serra nell'atmosfera, i quali a loro volta vanno ad amplificare l'effetto serra naturale: è un circolo vizioso.
Dunque è il nostro uso smodato di sostanze inquinanti a determinare il surriscaldamento globale: una piccola prova: basta guardare il nostro "pianeta gemello" Venere.
Venere ha un'atmosfera ricchissima di CO2: tutto ciò determina un effetto serra così forte che la sua temperatura in superficie può oltrepassare i 460 °C, ossia superare anche la temperatura del pianeta più vicino al Sole: Mercurio!
L'auspicio sarebbe dunque quello di ridurre la produzione di gas serra, sostituendoli con fonti di energia rinnovabili e non inquinanti: energia solare, eolica, da fissione nucleare (anche se in questo ultimo caso bisogna stare comunque attenti al problema scorie radiattive) o addirittura, in futuro, da fusione nucleare (non è certa la realizzazione: riprodurre il processo di fusione nucleare (processo tipico delle stelle) sulla Terra non è cosa facile), ecc.
Dato che abbiamo trattato l'effetto serra, possiamo andare anche ad analizzare il fenomeno di propagazione di calore che lo contraddistingue: l'irraggiamento.
L'irraggiamento è uno dei principali metodi di trasmissione del calore.

Ma vi sono altre 2 tipologie fondamentali:

1) conduzione: meccanismo di propagazione del calore con trasporto di energia ma senza alcuno spostamento di materia, da un corpo caldo a uno più freddo (2° principio della termodinamica). Risponde alla legge: Q/Δt = λSΔT/d, dove:

- Q/Δt è il calore trasferito (Q) in un intervallo di tempo (Δt);
- λ è il coefficiente di conducibilità termica, il quale dipende dalla sostanza di cui è fatta la regione di materia considerata. Inoltre si misura in (W/m · K);
- S = l'area dello strato di materia dove avviene il passaggio di calore
- ΔT è la differenza di temperatura sussistente tra i 2 corpi considerati;
- d = spessore

2) convezione: trasferimento di energia con trasporto di materia, dovuto alla presenza di correnti nei fluidi. Per capire meglio come funziona, consideriamo una pentola colma d'acqua posta su un fornello. L'acqua che è direttamente a contatto con il fondo della pentola si dilata, diventando meno densa di prima. A causa della famosa spinta di Archimede tale acqua tende a salire, generando così una corrente convettiva ascendente. L'acqua che sale viene, nel frattempo, sostituita da altra acqua più fredda, che scendendo verso il basso, crea una corrente convettiva discendente. In questo modo anche quest'acqua più fredda giunge vicino alla fonte di calore e si scalda, per poi risalire a portare calore in altre zone della pentola.

Ritornando al tema chiave, l'irraggiamento, invece, è descritto dalla legge di Stefan-Boltzmann:

I = εσST⁴, dove:

- ε = coefficiente di emissione (o di assorbimento). Il coefficiente è sempre compreso tra 0 e 1. Nel caso in cui ε=1, il corpo emittente considerato è un corpo nero;
- σ = costante di Stefan-Boltzmann che è pari a 5,6703 · 10^-8 W/(m² · K⁴);
- S = superficie del corpo interessata alla radiazione;
- T = sua temperatura.

Andiamo brevemente ad analizzare il caso del corpo nero.
Il corpo nero è un sistema fisico costituito da una cavità con un piccolissimo foro, tale che la radiazione che vi entra ha una bassissima probabilità di uscire.
Esso dunque riesce ad assorbire perfettamente e totalmente la radiazione entrante.
Nel 1860, il fisico tedesco Kirchhoff dimostrò che una cavità si comporta alla stregua di un corpo nero se:

- le pareti della cavità si trovano a temperatura T costante (temperatura del corpo nero);
- nella cavità è praticato un foro le cui dimensioni sono trascurabili rispetto a quelle del corpo stesso.

Questa cavità si comporta altrettanto bene come corpo nero nel caso in cui vengano scaldate le pareti: esse infatti rispondono emettendo radiazione, comportandosi così da perfetto radiatore.
La frazione di energia che fuoriesce dal minuscolo foro contiene tutte le frequenze della radiazione causata dal riscaldamento delle pareti.
Essa prende, non a caso, il nome di radiazione di corpo nero: dipende esclusivamente dalla temperatura delle pareti.
Un forno a pareti isolanti, dotato di un piccolo foro, si può considerare a tutti gli effetti un corpo nero.
Il corpo nero ha una particolare importanza perché sta alla base della nascita della meccanica quantistica.
Infatti, numerose erano le difficoltà che aveva la fisica classica (termodinamica ed elettromagnetismo) nello spiegare l'effettivo comportamento di questo sistema termico-radiativo, in quanto le previsioni classiche erano sì in accordo con i dati sperimentali, ma solamente nella regione della radiazione elettromagnetica a piccole lunghezze d'onda (ossia a bassa frequenza).
Fu il noto Max Planck, in una sua pubblicazione del 1900, a risolvere il problema del corpo nero, mostrando che le onde elettromagnetiche non assorbono energia in maniera continua, ma discreta e dando vita al concetto di quanto di energia.
Da quel momento in poi, si svilupperà la meccanica quantistica, che eliminerà qualsiasi certezza raggiunta dalla fisica classica.
In questo contesto, è necessario sottolineare l'importanza che ha avuto tale teoria (uno dei capisaldi della fisica del XX secolo) nello sviluppo della chimica.
Quest'ultima si è potuta implementare solo grazie al miglioramento del modello dell'atomo, all'introduzione degli orbitali, all'equazione di Schrödinger, al principio di esclusione di Pauli, rappresentanti solo alcuni dei principi base della teoria quantistica.
Tutta la chimica moderna, compresa l'importantissima chimica organica (o chimica del carbonio) si basa sulle leggi "bizzarre" della meccanica quantistica.
Solo per fare un esempio, la straordinaria capacità dell'atomo di carbonio di legarsi a se stesso mediante legami semplici, doppi o tripli si può spiegare solo facendo riferimento agli orbitali ibridi, concetti assolutamente non presenti nella fisica classica.
Si definisce semplicemente orbitale, la regione di spazio dove c'è oltre il 90% di probabilità di scovare l'elettrone, ma non c'è la certezza di trovarlo (100%).
Ecco la crisi di tutte le certezze, di tutte le convinzioni: il mondo della chimica (quello degli atomi, delle molecole, dei legami chimici, ecc.) è probabilistico e non deterministico.
Una vera e propria "Rivoluzione Copernicana" direbbe Kant!
Abbiamo quindi osservato come lo stesso progredire della chimica sia dipeso dalla fisica: tali discipline sono come 2 facce della stessa medaglia: non possiamo considerare una materia scientifica completamente staccata da un'altra: questo è il bello della scienza: essa è allo stesso tempo "infinita" nelle sue sfaccettature e "unica" in quanto onnicomprensiva.
Dopo questo excursus sulla meccanica quantistica, ritorniamo all'effetto serra e specialmente agli effetti che si porta dietro: il cambiamento climatico.
Come abbiamo notato in precedcenza, l'effetto serra, coadiuvato dall'inquinamento prodotto dall'uomo, incrementa la temperatura del nostro pianeta in maniera troppo eccessiva e in questo modo, si alimentano eventi estremi e catastrofici.
Primi tra tutti gli uragani: basti pensare che questi ultimi si nutrono del calore latente degli oceani.
Se noi andiamo ad aumentare le temperature degli oceani, il risultato sarà inevitabilmente uragani più forti (ricordiamo che i cicloni tropicali si misurano con la scala Saffir-Simpson) e anche più frequenti.
Esistono inoltre previsioni alquanto catastrofiche riguardo gli effetti della combinazione tra effetto serra naturale e inquinamento artificiale: lo scenario peggiore fa riferimento addirittura a una nuova piccola era glaciale.
Questa potrebbe essere causata dal suo fenomeno antitetico, ossia lo scioglimento dei ghiacci.
Partiamo da questo punto: più si incrementa la temperatura e più i ghiacciai si sciolgono.
Inoltre, questi ultimi, essendo una sorta di specchio riflettente delle radiazioni solari, nel caso iniziassero a sciogliersi, la nostra "barriera riflettente" sarebbe sempre meno efficiente, e così il ritmo di scioglimento si velocizzerebbe sempre più: una sorta di circolo vizioso.
Alcuni climatologi affermano che se si sciogliesse gran parte del Polo Nord, le acque fredde e dolci andrebbero a disturbare l'equilibrio oceanico, arrivando persino a bloccare la Corrente del Golfo, il cosiddetto "nastro trasportatore" del Nord Atlantico.
Con l'arresto di quest'ultima, si assisterebbe al fenomeno inverso rispetto al surriscaldamento globale: una sorta di piccola era glaciale nel Nord Europa.
Tirando le fila del discorso, giocare con i gas serra potrebbe portare alla rovina dell'uomo.
In altre parole, giocare (in maniera sconsiderata) con la chimica portebbe effetti, sulle dinamiche fisiche della nostra atmosfera e del nostro ambiente, inarrestabili e devastanti: nature always wins!



CONCLUSIONE

Abbiamo analizzato alcuni fenomeni riguardanti l'ambiente e in particolare l'atmosfera, riscontrando in essi particolari rapporti e legami tra fisica e chimica: forse, però, la più importante constatazione da fare è questa: fisica e chimica sono 2 figli di una disciplina senza la quale esse non potrebbero esistere, o quantomeno, esprimersi, ossia la matematica, che, a detta di Galileo, è il linguaggio con cui si presenta l'intero Universo.
In conclusione, ricordiamo che il 2011 sarà l'Anno Internazionale della Chimica, celebrativo delle importanti conquiste di tale disciplina e dei suoi innumerevoli contributi al benessere dell'umanità e all'evoluzione della scienza moderna.

IL CAMPO ELETTRICO: IL TEOREMA DI GAUSS

Andiamo ad analizzare un importante teorema inerente l'elettromagnetismo, che rappresenta la prima delle 4 equazioni di Maxwell: il Teorema di Gauss.
Prima di far ciò dobbiamo introdurre il concetto di campo elettrico.

IL CAMPO ELETTRICO

La forza elettrica che si genera tra 2 cariche elettriche, che possono essere, per quanto riguarda il segno, concordi (ossia tutte e 2 positive o negative) o discordi (una negativa e una positiva), ci è data dalla nota Legge di Coulomb, che prende la sua denominazione dallo scienziato francese Charles Augustine de Coulomb:



dove:

- F = forza elettrica;
- q1q2 = prodotto delle cariche;
- d² = distanza tra le cariche al quadrato;
- k = costante che vale 8,99 x 10⁹ N · m²/C².

Bisogna tuttavia dire che generalmente la costante k viene espressa in maniera più rigorosa mediante il rapporto 1/4πε0, dove ε0 (costante dielettrica nel vuoto) = 8,854 · 10-¹² C²/N · m².
Ora dobbiamo affermare che tale forza è una cosiddetta forza a distanza, nel senso che le 2 cariche risentono della forza attrattiva o repulsiva, anche se si trovano in 2 punti distanti, che possono essere separati da spazio vuoto di materia.
Riscontriamo dunque delle analogie tra la forza elettrica e quella gravitazionale: entrambe dipendono da leggi che presentano il prodotto di 2 grandezze (masse e cariche elettriche) divise per il quadrato della distanza tra i 2 corpi considerati, ed entrambe sono forze a distanza.
Compiamo un brevissimo excursus sulla gravità: essa rappresenta, seguendo la Relatività Generale di Einstein, la curvatura dello spazio-tempo determinata da un corpo, poniamo il Sole, che, proprio tramite tale deformazione del tessuto spazio-temporale, mette in moto i pianeti intorno ad esso, anche se molto distanti.
Si va quindi ad introdurre il concetto di campo.
In questo specifico frangente, tratteremo con particolare attenzione il campo elettrico.
Il concetto di campo elettrico viene introdotto partendo da alcune idee fondamentali:

• quando è presenta una carica elettrica Q1, essa modifica lo spazio che la circonda. Più precisamente, va a cambiare le proprietà in un punto B, in cui è situata una seconda carica, che chiamiamo Q0;
• questa seconda carica Q0 avverte una forza elettrica, che è dovuta proprio alle nuove proprietà dello spazio in cui essa si trova.
  

Pertanto, la carica Q1 è quella che genera un campo elettrico, mentre la zona dello spazio in cui si risentono gli effetti delle forze elettriche è detta sede del campo elettrico.
La seconda carica Q0 è solamente un escamotage che ci permette di constatare che nel punto B esiste un campo elettrico, ma esso esisterebbe comunque, anche se non ci fosse tale carica a rilevarlo.
La seconda carica Q0, generalmente, viene denominata carica di prova, proprio perché ci consente di studiare agevolmente il concetto di campo elettrico.
Questa carica di prova è scelta convenzionalmente abbastanza piccola, in modo da non andare a modificare in maniera rilevante, a causa delle forze da essa generate, il sistema fisico che si sta considerando.
A questo punto giungiamo ad introdurre quella grandezza che descrive la forza elettrica in ogni punto dello spazio: il vettore campo elettrico: E = F/Qo dove:

- E = vettore campo elettrico;
- F = forza di Coulomb;
- Q0 = carica di prova.

Specifichiamo che il vettore campo elettrico si misura in newton/coulomb (N/C).
Da tale relazione possiamo ricavare, attraverso semplicissimi passaggi, un'ulteriore equazione importante: F = E · Q, la quale ci permette di calcolare il valore della forza F che agisce su qualsiasi carica Q.
Partendo adesso dalla legge di Coulomb e dalla definizione di vettore campo elettrico, si può giungere a una formulazione più rigorosa del campo elettrico generato da una singola carica puntiforme.
Se andiamo a sostituire alla F della relazione E = F/Q0, la forza di Coulomb, mediante opportune semplificazioni otteniamo che il campo elettrico E di una carica puntiforme è uguale a:

E = kQ/d².

Se, invece, il campo elettrico è generato da più cariche puntiformi, andiamo ad utilizzare il principio di sovrapposizione, ossia giungiamo ad addizionare gli effetti delle varie cariche con la famosa regola del parallelogramma o col metodo punto-coda inerenti i vettori.
Detto ciò, cerchiamo di rispondere a una domanda: come si rappresenta il campo elettrico?
Compiamo un piccolo esperimento: immergiamo in un contenitore colmo d'olio una sferetta elettrizzata; cospargendo successivamente la superficie dell'olio con minuscoli frammenti di materiale dielettrico (isolante), si può osservare che questi ultimi si dispongono a raggiera intorno alla sfera.
I frammenti, sotto l'azione della forza elettrica, si polarizzano e si orientano, in ogni punto, parallelamente al campo.
Dunque si vanno a definire le linee del campo elettrico o linee di forza (introdotte dal fisico Michael Faraday, più noto per la scoperta dell'induzione elettromagnetica): linee orientate la cui tangente, in ogni punto, è diretta come il vettore campo elettrico in ciascun punto.
L'insieme delle linee ci dà un'idea generale dell'andamento del campo stesso.
Ora andiamo al nocciolo della questione: il Teorema di Gauss.
Prima di descrivere tale teorema, è necessario introdurre un importante concetto riguardante il campo elettrico, ossia il flusso del campo elettrico.
Esso è definito, nel caso in cui la superficie e il campo elettrico siano considerati uniformi, come:

Φ = E · n · S (= E · S cosα, in quanto prodotto scalare), dove:

- Φ = flusso del campo elettrico;
- E = vettore campo elettrico;
- n = versore (adimensionale) perpendicolare alla superficie considerata;
- S = area delle superficie dove si riscontra un flusso del campo elettrico.

L'unità di misura del flusso del campo elettrico è N · m²/C.
Se, al contrario, la superficie attraverso cui calcolare il flusso, risultasse non uniforme, curva, è necessario suddividere tale superficie in tanti elementi di area ΔS, sufficientemente piccola, in modo che tutti possono essere ritenuti piani e sui punti di ciascuno di essi il campo si possa ritenere approssimatamente uniforme.
Considerando la sommatoria di tutti i flussi parziali si arriva alla formula:

Φ = ∫E · n dS: la sommatoria tende all'integrale di superficie del vettore campo elettrico.
In particolare, dS indica l'area infinitesima degli elementi che idealmente compongono la superficie.
A questo punto si può definire il Teorema di Gauss (prende il nome dal celebre matematico Karl Friedrich Gauss, l'unico, insieme ad Eulero, ad essere stato definito "princeps mathematicorum"), che altro non è che un'altra maniera di esprimere il flusso del campo elettrico; in primo luogo forniamo una definizione più semplicistica: il flusso Φ del campo elettrico E attraverso una superficie chiusa è uguale alla somma algebrica delle cariche contenute all'interno della superficie, diviso la costante elettrica del mezzo in cui si trovano le cariche.
Nel caso specifico in cui le cariche sono situate nel vuoto si ha:

Φ = ∑Qi/ε0

Specifichiamo che questo teorema è valido quasi ovunque.
Tuttavia, la formula data andrebbe espressa in maniera più rigorosa, mediante un più elevato formalismo matematico, come poi la troviamo nel sistema di 4 equazioni differenziali alle derivate parziali di Maxwell.
Quindi, tale formula, in termini differenziali, diventa:

∇ · E = ρ/ε0

Il simbolo ∇ (nabla), chiamato anche del, una delta rovesciata, rappresenta un'antica arpa assira di forma triangolare.
Il nome "nabla" fu coniato da William Hamilton nel 1837; Maxwell avrebbe preferito dare a questo operatore differenziale il nome di "pendenza".
Considerando uno spazio tridimensionale, il ∇ riunisce le pendenze (le derivate parziali) nelle varie direzioni.
Precisamente, applicandolo a una funzione f(x,y,z), si ottiene un campo vettoriale g(x,y,z) con componenti:

- g1 = ∂F/∂x;
- g2 = ∂F/∂y;
- g3 = ∂F/∂z.

Ritornando al teorema di Gauss, il simbolo ρ indica la densità di carica volumetrica, mentre la notazione ∇ · E rappresenta un prodotto scalare, o ancor più precisamente, la divergenza (div E) del campo elettrico.
La divergenza è un operatore che misura la tendenza di un campo vettoriale a divergere o convergere verso un punto del campo stesso.
Se, per esempio, immaginiamo un campo vettoriale bidimensionale che rappresenta la velocità dell'acqua, contenuta in una vasca da bagno che si sta svuotando, la divergenza avrebbe:

- valore negativo: nelle vicinanze dello scarico, visto che in quel punto l'acqua sparisce, se ne va via;
- valore prossimo allo zero: lontano dallo scarico, in quanto riscontriamo che in quei punti la velocità dell'acqua sarebbe quasi costante.

Se supponiamo l'acqua incomprimibile in una data regione dello spazio, nella quale non sono presenti nè pozzi di scarico nè sorgenti d'acqua, allora possiamo dire che la divergenza del campo delle velocità sarà ovunque nulla.
Un campo vettoriale che abbia come caratteristica particolare quella di avere divergenza nulla ovunque, viene detto soleinodale.
Lo stesso campo magnetico, descritto anch'esso dalle equazioni di Maxwell, si può considerare un campo soleinodale: in tale campo non si riscontrano sorgenti.
Tirando le fila del discorso, abbiamo illustrato il primo passo importante verso la completa comprensione dell'intero sistema delle equazioni di Maxwell, la sintesi perfetta di una grande e importante branca della fisica nota come elettromagnetismo.

BREVE ANALISI SULLA DIDATTICA DELLA SCIENZA NELLA SCUOLA

La didattica della scienza (matematica, fisica, astronomia, chimica, ecc.) nella scuola = sicuramente qualcosa da sviluppare, implementare, migliorare.
Non a caso, molte volte, le materie scientifiche risultano, agli occhi degli studenti, le più complicate e difficili.
Ci sono persino alcuni che affermano in maniera netta e convinta: "io sono negato per la matematica e per la fisica"!
Dunque, sorge una domanda: è vero che tali materie sono effettivamente complicate di per sé e quindi possono essere capite soltanto da invidui appassionati, con una predisposizione per esse, oppure, in realtà, è il fatto di spiegarle, illustrarle il più delle volte in maniera non efficace, a renderle qualcosa di inaccessibile a molti studenti?
Su tale tematica, vorrei far riferimento al film "L'amore ha due facce" con Barbra Streisand e Jeff Bridges: in tale pellicola cinematrografica troviamo:

- una docente di letteratura alla Columbia University di New York, che compie delle lezioni assolutamente magistrali, che vanno a trascinare gli ascoltatori, tanto da essere applaudita calorosamente;
- un professore di matematica, sempre alla Columbia University, che poi si innamora della collega; questo insegnante, al contrario della sua amata, fornisce delle spiegazioni ai suoi studenti che risultano noiose, soporifere e incomprensibili, per chi non è letteralmente "innamorato" della sua materia. Vengono criticati anche i suoi libri redatti sulla cosidetta "ipotesi dei primi gemelli", che considera le coppie di numeri primi separati da 2 unità tra loro.

Andando al nocciolo della questione, in una splendida ed esilarante scena del film, il professore tiene una sorta di lezione alla docente di letteratura, la quale lo invita, nel momento in cui spiega, a non comportarsi come se fosse l'unico partecipe della lezione di matematica: lei lo incita a cercare di raccontare gli stessi argomenti in una maniera più coinvolgente.
Il personaggio interpretato da Barbra Streisand arriva addirittura ad invitare Jeff Bridges a raccontare una "storia", una "favola" nella spiegazione di un'equazione matematica (nella scena si parla precisamente del limite cui tende la velocità in una data equazione, quando l'intervello di tempo t tende a 0), ma lui si rivela assolutamente incapace di fornire un racconto accattivante.
In seguito, tuttavia, l'insegnante di matematica, sotto consiglio della docente di letteratura che diventerà sua sposa, introduce nella sua lezione l'evento della partita di baseball, che era stata giocata il giorno immediatamente precedente, spiegandolo in termini matematici e fisici.
Quegli stessi studenti che nelle lezioni, fino a quel momento, si erano dimostrati come assolutamente non interessati alla spiegazione, improvvisamente, come un fulmine a ciel sereno, cominciano ad ascoltare con attenzione il discorso del professore!
Tutto questo fa capire che la comprensione e l'interessamente a riguardo della scienza cambia in modo esorbitante, a seconda se la spiegazione fornita dal docente è accattivamente, moderna, divertente o, al contrario, noiosa e rindondante.
Detto ciò, direi di stabilire alcuni punti fondamentali per far sì che gli studenti si appassionino o almeno studino con un po' d'interesse le scienze, senza affermare frasi del tipo: "non mi serve a niente conoscere le formule di Prostaferesi", "cosa me ne farò mai del Teorema di Gauss?", "a cosa mi serve sapere cosa è la derivata di una funzione?" e molte, moltissime altre ancora:

1) rendere le lezioni più accattivanti, basandosi sul modello di Barbra Streisand e non su quello di Jeff Bridges!: anzi io penso che sia più semplice rendere più interessante una lezione di matematica, fisica, o di scienza in generale, piuttosto che una di letteratura, dato che la scienza permette di offrire più spunti nella realtà quotidiana rispetto a una poesia;
2) riprendendo il primo punto, bisognerebbe soffermarsi su come la scienza ci descrive la realtà e nel mostrare che tutto ciò che circonda è descrivibile con il linguaggio matematico. è necessario, dunque, fare più riferimenti alla realtà quotidiana, per far vedere che la matematica non è solo un linguaggio fatto di formule, numeri, lettere e che essa è fine a se stessa, ma anzi, essa è la stessa essenza delle cose. Se qualcuno dice "non mi piace la matematica", allora, a rigor di logica, non dovrebbe usare cellulari, computer, lettori mp3 e tecnologie simili, in quanto il loro funzionamento dipende proprio dalla matematica. Per far scaturire l'interesse, ad esempio, per la fisica, si potrebbe anche far riferimento al mondo dei fumetti, come è chiaramente visibile nel libro "La fisica dei supereroi di James Kakalios".
3) si dovrebbe introdurre nelle scuole un minimo di storia della scienza, poiché è utile per capire come si è giunti a formulare le teorie fisiche, i teoremi matematici e tutte le altre leggi della scienza, altrimenti si potrebbe affermare che "queste formule sono uscite dal nulla", senza conoscere lo sforzo (lo "streben" fichtiano) di numerosi scienziati, che c'è dietro. Perché ci ricordiamo subito il ruolo di Newton nella scoperta della gravità? perchè abbiamo in mente l'immagine della mela che cade in testa allo scienziato;
4) bisognerebbe visionare molti documentari, di quelli ben realizzati, in quanto molto spesso l'immagine colpisce più della parola. Un esempio lampante di tale considerazione: uno studente ricorderebbe nel tempo più, cos'è un vulcano e quali sono le sue caratteristiche, leggendo la sua descrizione, oppure visionando un documentario, dove si possono osservare veramente le fasi dell'esplosione di questa "montagna di fuoco"?
5) i programmi scolastici dovrebbero probabilmente essere più orientati verso argomenti che possano veramente interessare i ragazzi: perchè in fisica, generalmente, non si riesce mai ad affrontare la relatività di Einstein o la meccanica quantistica, pur essendo, molto interessanti e stimolanti?. Si potrebbe rispondere: "queste 2 branche della fisica sono troppo complicate (sono necessari strumenti matematici molto elevati) per essere comprese dai giovani studenti", ma io penso che tutti gli argomenti, persino quelli più difficili, possono essere illustrati con semplicità e con incisività. Il ruolo dell'insegnante dovrebbe essere quello di spiegare in maniera comprensibile anche quei concetti che possono sembrare inaccessibili ai non addetti ai lavori. Einstein, diceva giustamente: "Non hai veramente capito qualcosa finché non sei in grado di spiegarlo a tua nonna".

Questi, a mio parere, sono alcuni tra i punti fondamentali che bisognebbe tenere presenti, per un insegnamento sempre migliore ed efficace di quella meravigliosa disciplina che è la scienza!
Infine, concludo con alcuni video inerenti il film precedentemente citato e le colonne sonore della medesima pellicola.
N.B: consiglio di guardare con attenzione la scena della magistrale lezione tenuta da Barbra Streisand (che tra l'altro nomina anche il termine "equazione", cosa che in lezioni di letteratura è molto difficile riscontrare; bisognebbe comprendere che la scienza è legata indissolubilmente anche all'arte e soprattutto alla musica, altra disciplina fortemente trascurata dalla scuola italiana) ai suoi allievi.