Per celebrare questo magico numero in questo post parleremo di un'importante formula in cui fa capolino pi greco.
Iniziamo la sua presentazione riportando un interessante passo da "Le grandi domande, Matematica" di Tony Crilly:
"L'onnipresenza dei computer nella vita moderna ha fatto sì che occorra un gran numero di formule nell'ambito della «combinatoria», la branca della matematica che calcola le possibili combinazioni di oggetti. Tre oggetti, diciamo a, b e c, danno luogo a 3 × 2 × 1 = 6 «permutazioni» (abc, acb, bac, bca, cab, cba) e fin qui non serve una formula. Ma se, ad esempio, stessimo considerando dieci oggetti, il numero di possibili permutazioni salirebbe a 3.628.800, e a un valore formidabile di 9,33 × 10¹⁵⁷ oggetti. Adesso chiaramente una formula ci risparmierebbe molta fatica. Ed è qui che viene in nostro aiuto la «formula di Stirling», così chiamata dal nome del matematico scozzese James Stirling. Che nella formula compaiano anche la costante π e la costante di eulero e è una sorpresa. La presenza di π, che in genere ha a che fare con le circonferenze, e di e, che ha a che fare con la crescita, ci ricorda i nessi sorprendenti che ci offre la matematica, a maggior ragione considerando che il problema originario riguarda solo la moltiplicazione di numeri interi. Eppure la formula è notevole anche per la bontà della sua approssimazione al valore effettivo: nel caso di 100 oggetti se ne discosta appena dello 0,083%."
Dunque, tirando le fila del discorso incominciato da Crilly, la formula di Stirling (detta anche approssimazione di Stirling o formula approssimata di Stirling o formula di Moivre-Stirling, giacché fu il francese de Moivre il primo a stabilirla, anche se con una costante diversa) fornisce la valutazione approssimata del fattoriale di un numero n › 0.
La formula venne presentata nella forma attuale nel 1730 da James Stirling (1692-1770) nella sua opera più importante, denominata Methodus differentialis.
Costui fu amico nientemeno che di Newton e aveva avviato la sua carriera da matematico tra conflitti religiosi e politici, tuttavia dopo il 1735 si dedicò principalmente alla gestione aziendale.
Ma qual è l'aspetto della suddetta formula?
Essa appare come un limite
Ma più comunemente viene scritta nel seguente modo:
ove n è appunto il numero di oggetti considerati.
Essa è sovente utilizzata nel calcolo di limiti di successioni e, di conseguenza, anche nello studio di serie numeriche o di potenze.
Consideriamo per esempio il semplice limite

Qui applicando la formula di Stirling possiamo riscrivere il limite come

ovvero:

Effettuando una semplice stima asintotica, è facile constatare che al crescere di n verso +∞ il denominatore, essendo un termine esponenziale, crescerà molto più rapidamente del numeratore.
Ergo, il limite è eguale a 0.
Risulta molto semplice ricavare la formula di Stirling in versione logaritmica.
Passando infatti ai logaritmi naturali, l'espressione diviene:
Ricordando le regole fondamentali relative ai logaritmi, che abbiamo visto qui, abbiamo che:
cioè
Questa è appunto la formula di Stirling in versione logaritmica.
Quando n però è molto grande, è possibile esprimerla in questo modo maggiormente sintetico:

Chiudiamo il post innanzitutto con una chicca, presentando uno straordinario estratto tratto dal recente "100 cose che NON SAPEVI di non sapere sulla MATEMATICA e le ARTI" di John D. Barrow, il quale ci parla di torte nuziali, ma fa capolino anche pi greco ovviamente:
 "Glassare le torte nuziali è un'arte sopraffina. La superficie del dolce dev'essere liscia, ma abbastanza resistente da sostenere gli strati soprastanti, e talvolta i delicati fiori di zucchero devono essere abbinati al bouquet della sposa. Ora consideriamo il problema di cuocere e glassare una torta nuziale particolarissima, che avrà molti strati, ognuno dei qual è un cilindro solido alto un'unità. A mano a mano che dal primo strato passiamo al secondo, al terzo e così via, fino all'ennesimo, le dimensioni dei cilindri diminuiranno: il primo avrà raggio 1, il secondo 1/2, il terzo 1/3, e il raggio del cilindro circolare che formerà lo strato n-esimo sarà 1/n. Il volume di un cilindro di raggio r e altezza h è semplicemente πr²h, perché è solo una pila di cerchi di area πr² fino all'altezza h. L'area della superficie esterna di questo cilindro è quella di una pila di cerchi di circonferenza 2πr, dunque pari a 2πrh. Queste formule ci dicono che il volume dell'n-esimo strato della nostra particolarissima torta sarà
"Glassare le torte nuziali è un'arte sopraffina. La superficie del dolce dev'essere liscia, ma abbastanza resistente da sostenere gli strati soprastanti, e talvolta i delicati fiori di zucchero devono essere abbinati al bouquet della sposa. Ora consideriamo il problema di cuocere e glassare una torta nuziale particolarissima, che avrà molti strati, ognuno dei qual è un cilindro solido alto un'unità. A mano a mano che dal primo strato passiamo al secondo, al terzo e così via, fino all'ennesimo, le dimensioni dei cilindri diminuiranno: il primo avrà raggio 1, il secondo 1/2, il terzo 1/3, e il raggio del cilindro circolare che formerà lo strato n-esimo sarà 1/n. Il volume di un cilindro di raggio r e altezza h è semplicemente πr²h, perché è solo una pila di cerchi di area πr² fino all'altezza h. L'area della superficie esterna di questo cilindro è quella di una pila di cerchi di circonferenza 2πr, dunque pari a 2πrh. Queste formule ci dicono che il volume dell'n-esimo strato della nostra particolarissima torta saràπ × (1/n²) × 1 = π/n²
e l'area della superficie esterna da glassare sarà pari a
2π × (1/n) × 1 = 2π/n.
Questi sono solo il volume e l'area dello strato n-esimo. Per calcolare il totale dell'intera torta di n strati dovremo sommare i volumi e le aree di tutti gli strati (1, 2, 3...n). Ora immaginiamo una particolarissima torta dal numero infinito di strati. Il volume totale sarà dato dalla somma dei volumi del numero infinito di strati:
Volume totale: π × (1 + 1/4 + 1/9 + 1/16 +...) =
La caratteristica straordinaria di questa somma infinita di termini («serie») è che è un numero finito. Il valore numerico dei termini della serie diminuisce abbastanza in fretta perché la serie converga su π²/6, che è circa 1,64. Ci occorrerebbero dunque solo una quantità finita di miscela per dolci per creare la nostra torta nuziale dal numero infinito di strati. Ora dobbiamo glassarla: abbiamo bisogno di sapere quanta glassa preparare e quindi di calcolare l'area della superficie esterna (ignoreremo la piccola regione anulare di larghezza 1/n -1/(n+1) lasciata su ciascuno strato da quello superiore). L'area totale da glassare è la somma delle aree di tutti gli strati della torre infinita:
Superficie totale: 2π × (1 + 1/2 + 1/3 + 1/4 +...) =

Questa somma [serie armonica] è infinita. La serie di termini 1/n non diminuisce abbastanza in fretta da convergere a una soluzione finita. Se si includono nella somma abbastanza termini, la si può rendere grande a piacere. È facile capirlo, perché la somma della serie deve essere maggiore di quella della serie
1 + (1/2) + (1/4 + 1/4) + (1/8 + 1/8 + 1/8 + 1/8) +...,
dove il successivo (...) conterrà otto 1/16 e il successivo (...) sedici 1/32. Ognuna delle somme tra parentesi vale quindi 1/2. Ce ne saranno naturalmente un numero infinito, poiché la somma della serie è pari a 1 più un numero infinito di metà, che è comunque sempre infinito. La nostra somma è maggiore di questa, quindi deve avere a sua volta una somma infinita: l'area della superficie della nostra torta infinita sarà infinita (ed ecco perché non ci siamo preoccupati di aggiungervi le regioni anulari di glassa sopra ciascuno strato). Questo risultato è incredibile e del tutto inaspettato: la ricetta della nostra torta infinita richiede una quantità finita di miscela per dolci, ma non potrà mai essere glassata perché ha una superficie infinita!"
E ora la chiusa definitiva in musica grazie a The Voice Frank Sinatra in "Love and Marriage":


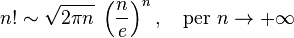























Nessun commento:
Posta un commento