Uno di loro, Luis, è divenuto uno studioso di statistica, esperto nel riconoscere le tendenze generali che si manifestano nei sistemi sociali, costituiti da numerosi elementi (per esempio, i movimenti di una popolazione).
Per far sì che Antonio riesca a comprendere meglio di cosa lui si occupi, Luis gli mostra un articolo che aveva lì con sé, nel quale viene descritta una distribuzione gaussiana, e prova a spiegargli i simboli usati per indicare la media della popolazione, la popolazione reale, ecc.
Antonio, che non ha una grande formazione scientifica alle spalle, rimane un tantino perplesso e inizia a sospettare che il suo vecchio amico lo stia prendendo in giro.
"Come puoi sapere queste cose?" chiede.
E rincara la dose con l'interrogativo: "E che simbolo è questo?".
Al che Luis risponde "Oh! Questo è π".
"E cosa rappresenta?" prosegue Antonio.
"Il valore che si ottiene dividendo la lunghezza di una circonferenza per il suo diametro" è la chiara risposta di Luis.
Ma Antonio è ancor più incredulo, tanto da asserire: "Ora sì che hai esagerato; cosa diavolo ha a che vedere la popolazione con la lunghezza di una circonferenza?".
Quella appena raccontata è una storiella frutto della mente del fisico ungherese, naturalizzato statunitense, Eugene Wigner, insignito del premio Nobel per la Fisica nel 1963 per "i suoi contributi alla teoria del nucleo atomico e delle particelle elementari, in particolare mediante la scoperta e l'applicazione di fondamentali principi di simmetria".
Il protagonista della vicenda appena narrata è il numero 3.14159...., il cui simbolo è l'inconfondibile π, che designa probabilmente l'emblema stesso della Matematica.
Sin da piccoli, a scuola, ci imbattiamo in questo "magico" numero irrazionale quando ci viene descritta la formula della lunghezza di una circonferenza o dell'area di un cerchio (a tal proposito, vi consiglio caldamente di guardare il seguente superlativo video).
Con il proseguire degli studi, lo ritroviamo nella geometria solida (per esempio, nell'equazione descrivente il volume di una sfera), nella goniometria e trigonometria, nell'analisi, nella statistica, nella fisica e così via (potete constatarlo nel post "Una galleria di formule dedicata a pi greco").
Pi is everywhere!
Infatti, rappresenta persino il titolo di una canzone di Kate Bush e il nome di un profumo di Givenchy.
Ma pi greco, oltre ad essere fondamentale in ambito scientifico, possiede anche una storia affascinante.
Andremo dunque, per celebrarlo in vista del Pi Day (14 marzo), ad analizzare le vicende ad esso legate e indagare sui principali protagonisti che hanno portato alla sua scoperta e alla sempre maggiore conoscenza delle sue infinite cifre.
Il simbolo greco π venne utilizzato per la prima volta nel testo A New Introduction to the Mathematics, nel 1706, dal matematico gallese (che fu peraltro vicepresidente della Royal Society) William Jones (1675-1749) per designare il rapporto sussistente tra la lunghezza di una circonferenza e il diametro.
Nella sua importante opera Introduzione all'analisi degli infiniti (1748), Eulero approvò tale uso di π, contribuendo così alla sua ampia diffusione.
Una precisazione: prima dell'arrivo di Jones, la suddetta lettera greca veniva sfruttata dai matematici per indicare la circonferenza.
Ma l'incipit della storia del pi greco ha origini decisamente più antiche!
Le prime approssimazioni di pi greco provengono addirittura dai babilonesi, che ne constatavano un valore pari a 25/8 (ossia 3,125), e dagli egizi, che osservavano un valore equivalente a (16/9)², cioè 3,1605.
Nello specifico, per quanto concerne gli egizi, ritroviamo il calcolo di π nel 1650 a.C. circa, all'interno del papiro di Rhind (di cui abbiamo parlato nell'introduzione del Carnevale della Matematica n.56).
Infatti, in esso viene calcolata l'area di un cerchio con un diametro di 9 unità ponendola uguale a quella di un quadrato con il lato di 8 unità.
Ciò implica un valore di pi greco appunto pari a circa 3,16.
Infatti, sappiamo che l'area del quadrato è:
.gif)
mentre quella del suddetto cerchio è:
Siccome l'area del quadrato e quella del cerchio devono risultare identiche, abbiamo che:
.gif)
Per quanto riguarda i babilonesi, nella tavoletta di Susa, risalente al 2000 a.C. circa, troviamo l'equiparazione di un esagono a un cerchio e, nel dettaglio, il rapporto tra il perimetro dell'esagono e la circonferenza, che restituisce un valore di pi greco pari a 3,125.
Perfino in un versetto della Bibbia si trova un accenno al pi greco: "Fece un bacino di metallo fuso di dieci cubiti da un orlo all'altro, rotondo; la sua altezza era di cinque cubiti e la sua circonferenza di trenta cubiti" (1 Re 7, 23).
Se la forma del bacino è un cerchio con una circonferenza di 30 cubiti e un diametro di 10, allora il valore di pi greco presente nella Bibbia è 30/10 = 3, un valore non molto preciso.
Nell'VIII secolo a.C. il matematico indiano Baudhayana formulò la seguente regola:
ove s indica il lato di un quadrato, mentre d il diametro di un cerchio.
Se le aree delle 2 figure sono identiche, allora l'uguaglianza appena scritta restituisce un valore di pi greco equivalente a circa 3,09.
Un tentativo di ottenere una stima maggiormente precisa fu effettuato da un astronomo e ideatore di calendari chiamato Liu Hsing, vissuto appena prima dell'inizio dell'era cristiana.
Incaricato dal re Wang Mang di costruire una misura standard di capacità, Liu Hsing progettò un recipiente cilindrico di bronzo che assunse il ruolo di prototipo di centinaia di recipienti prodotti e distribuiti in Cina.
Dopo aver osservato le dimesioni di uno dei recipienti (conservato attualmente in un museo di Pechino), alcuni commentatori hanno ipotizzato che il matematico fece uso del valore
.gif)
Supposizione supportata da un'annotazione contenuta nel Sui Shu (cioè nella Storia ufficiale della dinastia Sui) in cui si dichiara che Liu Hsing aveva trovato un nuovo valore per pi greco in sostituzione del vecchio 3.
Il primo trattato sistematico sull'argomento, redatto nel III secolo d.C., è contenuto nell'importantissimo commentario del matematico Liu Hui all'opera Nove capitoli sulle arti matematiche (ne abbiamo parlato qui).
Costui incominciò esaminando l'ipotesi di base nei problemi n.31 e 32 del primo capitolo, dove l'area di un cerchio veniva calcolata prendendo il prodotto di metà della circonferenza e di metà del diametro.
Dopo aver illustrato i fondamenti logici di tale regola e di questo uso del valore impreciso 3 come rapporto fra circonferenza e diametro, Liu espose un suo metodo atto ad ottenere un valore maggiormente accurato per π.
Il suddetto metodo è abbastanza simile a quello che il grande Archimede aveva sviluppato circa 400 anni prima (nel 250 a.C. circa).
Praticamente, il genio siracusano disegnò innanzitutto un cerchio (di raggio 1) e dopodiché raffigurò 2 esagoni, uno inscritto nel cerchio e uno circoscritto al cerchio.
Archimede applicò dunque il famoso metodo di esaustione, che consiste appunto nell'inscrivere e circoscrivere poligoni attorno ad una figura geometrica piana ed aumentare progressivamente il numero di lati del poligono affinché approssimi il più possibile la linea curva.
Archimede, partendo dall'esagono regolare (poligono a 6 lati), arrivò a considerare 2 poligoni regolari (uno inscritto e l'altro circoscritto alla circonferenza) di ben 96 lati, passando per quelli di 12, 24 e 48 lati.
Soffermiamoci un attimo sull'esagono regolare.
Per capire meglio le sue caratteristiche, teniamo come riferimento la seguente immagine, illustrante una circonferenza in cui è inscritto un esagono regolare, che a sua volta circoscrive un'altra circonferenza più piccola.

Il raggio della circonferenza inscritta nell'esagono (ovvero quella al suo interno) è ovviamente detto apotema ed è anche esprimibile attraverso un'equazione, sfruttando il teorema di Pitagora.
Infatti, possiamo considerare il triangolo equilatero (suddiviso in 2 triangoli rettangoli) in figura e scrivere la seguente uguaglianza:
.gif)
ove a indica l'apotema, mentre l il lato dell'esagono.
Da ciò posso facilmente ricavare che:
.gif)
Ma come si calcola l'area di un esagono regolare?
Semplice: non è altro che perimetro per apotema diviso 2.
Scriviamola in termini maggiormente rigorosi:
.gif)
Ma il perimetro P non è altro che la misura del lato moltiplicata per 6!
Ergo:
.gif)
Ora possiamo anche andare a sostituire l'espressione ricavata in precedenza dell'apotema:
Ecco a voi l'area di un esagono regolare!
Nel nostro caso (cioè nella procedura di Archimede), dove abbiamo una circonferenza di raggio 1 circoscritta a un esagono regolare, otteniamo ovviamente che il lato l dell'esagono è uguale a 1 (riguardate la figura sopra se avete perplessità) e quindi l'area dell'esagono inscritto è:
.gif)
Archimede riuscì incredibilmente a calcolare tutte le aree dei poligoni (ricordo, fino a 96 lati) inscritti e circoscritti alla circonferenza!
Costruiamo dunque una piccola tabella:

Come potete osservare, man mano che il numero di lati dei poligoni aumenta, il valore delle loro aree si avvicina sempre più a quello di π.
Scrivendo il tutto in termini matematici odierni, se indichiamo con
e con
rispettivamente inscritti e circoscritti alla circonferenza, allora possiamo affermare che:
Che diavolo significa?
Non vi preoccupate, nulla di complicato!
Per comprenderne il significato, dobbiamo introdurre alcuni facili concetti: massimo, minimo, maggiorante, minorante, estremo superiore ed estremo inferiore.
Consideriamo un insieme A di numeri reali.
Se esiste, il massimo di A non è altro che un numero M dell'insieme A che risulta superiore o uguale ad ogni altro elemento di A.
Scritto in termini formali:
Allo stesso modo, il minimo di un insieme A è un numero m dell'insieme stesso che risulta minore o uguale a tutti gli altri elementi di A.
In simboli:
Non tutti gli insiemi di numeri reali possiedono un massimo e un minimo.
Se, ad esempio, A risulta formato da tutti i numeri reali positivi, non esiste né un massimo (ovvio!) né un minimo (non esiste infatti il più piccolo numero reale positivo).
Una proprietà ovvia è che quando max e min esistono, allora risultano unici.
Proseguendo oltre, si definisce maggiorante per un insieme A di numeri reali un certo numero reale L (NOTA BENE: L non necessariamente appartiene all'insieme A, a differenza di quanto accadeva nella definizione di massimo) tale che:
.gif)
per ogni numero a appartenente all'insieme A.
Alla stessa stregua, un numero reale l viene detto minorante di A se:
.gif)
per ogni a ∈ A.
Bisogna precisare che un insieme A di numeri reali non sempre ammette maggioranti e minoranti.
Se consideriamo A nuovamente come l'insieme dei numeri reali positivi, allora sicuramente esso non ammette un maggiorante, poiché non è possibile trovare un numero reale che sia più grande di tutti quanti gli elementi di A, mentre ammette un minorante, che può essere lo 0, così come qualsiasi numero reale negativo.
Da ciò consegue che un insieme che ammette un maggiorante viene chiamato limitato superiormente, mentre uno che ammette un minorante è denominato limitato inferiormente.
Se l'insieme ammette sia un maggiorante che un minorante, allora viene detto semplicemente limitato.
Detto ciò, si possono definire i concetti di estremo superiore ed inferiore.
Se A è un insieme di numeri reali non vuoto e limitato superiormente, diciamo che M ∈ R (R è l'insieme di tutti i numeri reali) è l'estremo superiore di A se M è il minimo (se volete, il più piccolo) dei maggioranti di A.
Sembra uno scioglilingua ma è un concetto molto importante!
Analogamente, se A è un insieme di numeri reali non vuoto limitato inferiormente, allora un numero reale m rappresenta l'estremo inferiore di A se m è il massimo (il più grande) dei minoranti di A.
Ed ecco che arriviamo al chiarimento della strana uguaglianza coinvolgente il pi greco.
L'estremo superiore di A viene indicato in forma abbreviata come sup A, mentre l'estremo inferiore come inf A.
Per chiarire definitivamente le idee, facciamo un semplicissimo esempio.
Immaginiamo di avere un insieme B definito nella seguente maniera:
.gif)
e di volerne stabilire il sup e l'inf.
Innanzitutto, possiamo notare che la disuguaglianza
.gif)
implica che:
.gif)
Pertanto, questo insieme B contiene tutti i numeri reali minori di 2.
Scritto in termini più rigorosi:
.gif)
Possiamo facilmente notare che esistono infiniti maggioranti (cioè numeri più grandi di qualsiasi elemento di B) per B, tra i quali il più piccolo è 2.
Ergo:
.gif)
Al contrario, non esistono minoranti (d'altronde non si possono trovare numeri più piccoli di -∞) e dunque non esiste nemmeno l'estremo inferiore di B.
Ora dovrebbe essere molto più comprensibile l'espressione:

Per maggiori informazioni sul metodo di Archimede, vi invito a leggere questo capolavoro di post scritto dai Rudi Matematici.
Ora passiamo al metodo di Liu Hui, a proposito del quale vi riporto la magnifica descrizione che ne compie George Gheverghese Joseph nel libro C'era una volta un numero:
"Archimede basò il suo metodo sulla semplice osservazione che, quando un cerchio è racchiuso tra 2 poligoni di n lati, se si aumenta n, la differenza tra la circonferenza del cerchio e i perimetri dei poligoni inscritti e circoscritti diminuisce di conseguenza, così che, in ultima istanza, aumentando a dismisura il numero dei lati, i perimetri dei poligoni e del cerchio finirebbero con il diventare identici. In altre parole, aumentando n, la differenza di area tra i poligoni e il cerchio dovrebbe gradualmente esaurirsi...Il metodo di Liu Hui per calcolare π necessitava solamente di poligoni regolari inscritti. Partendo dal perimetro conosciuto di un poligono regolare di n lati inscritto in un cerchio, veniva calcolato il perimetro di un poligono regolare inscritto di 2n lati applicando il teorema di Pitagora 2 volte. Il cerchio nella figura
ha il centro in O e il raggio r. Sia PQ = s il lato di un poligono regolare inscritto di n lati con un perimetro conosciuto. Quindi, dati s e n, si usa il teorema di Pitagora per calcolare di volta in volta che:
.gif)
.gif)
.gif)
dove w è uno dei 2n lati del poligono regolare. Una ripetizione di questo procedimento produrrà approssimazioni sempre più vicine alla circonferenza del cerchio, condizioni che permettono quindi una definizione di π. Con i poligoni circoscritti si può usare un procedimento simile. Nell'esempio di Liu OR = r = 10, n = 6 e PQ = s = 10, e in questo modo
.gif)
La prima iterazione produce
.gif)
che è la lunghezza del lato di un poligono regolare di 12 lati. La ripetizione dello stesso processo per un poligono di 12 lati con s = 5,176381 dà
.gif)
Continuiamo il processo iterativo fino a quando viene trovata la lunghezza del lato di un poligono regolare di 96 lati. Ora l'area di un poligono regolare inscritto di 2n lati è
.gif)
dove s è la lunghezza del lato di un poligono con n lati e r è il raggio del cerchio. A causa delle dimensioni fornite sopra
è l'area di un poligono di 12 lati e similmente:
è l'area di un poligono di 24 lati. Proseguendo su questo tracciato, Liu trovò che
.gif)
Grazie a una argomentazione geometrica egli dimostrò che
dove A è l'area del cerchio. Questo porta a
.gif)
e grazie a una interpolazione Liu Hui giunse quindi a
.gif)
Al pari di Archimede, egli racchiuse questo risultato tra 2 limiti."
George Gheverghese Joseph prosegue poi la narrazione sul calcolo del pi greco nell'antica Cina con le seguenti parole:
"La passione dei cinesi per la determinazione del valore di π raggiunse i massimi livelli nell'opera di Tsu Chung-Chih e di suo figlio Tsu Kêng-Chih, che stabilirono nuovi confini per questo valore. Nel testo intitolato Sù Shu (Metodo di interpolazione), scritto nel 479 d.C. ma oggi introvabile, il vecchio Tsu può aver probabilmente spiegato il suo metodo per dare un'approssimazione a π. Tutto quello che ci rimane sono brani contenuti nella Storia ufficiale della dinastia Sui, che riportano gli sforzi di Tsu (che viene descritto come uno storico) per migliorare la precisione del valore di π. Utilizzando un cerchio di diametro 10 chih, suddiviso in 10⁸ unità, egli trovò per π un limite superiore di 3,1415927 e un limite inferiore di 3,1415926. Nello stesso testo si dichiara che Tsu fornì 2 valori di π, uno impreciso pari a 22/7 (valore di Archimede), e uno esatto, pari a 355/113, esatto alla sesta cifra decimale, che appare nelle opere dei matematici indiani del XV secolo. Nel 1585 un matematico olandese, Adrien Anthoniszoon, scoprì questo valore, a quanto pare sottraendo i numeratori e i denominatori dei valori di Tolomeo [II secolo d.C.] e di Archimede, 377/120 e 22/7! L'ipotesi più verosimile è che la conoscenza indiana ed europea di questo valore di π così preciso provenga dalla Cina, poiché la scoperta di Tsu si trasmise nel corso di molti secoli verso sud e verso ovest. In Cina però l'opera di Liu e Tsu fu presto dimenticata e continuarono a essere utilizzate approssimazioni imprecise, non escluso il semplice 3. Nel 1247 Chhin Chiu-Shao affermò che 3, 22/7 e radice quadrata di 10 [valore calcolato dall'indiano Brahmagupta nell'VII secolo d.C.] erano tutte utilizzate! Nel 1275 Yang Hui elaborò 5 formule per calcolare l'area di un cerchio. In una π era uguale a 3, due utilizzavano 22/7 e nelle due rimanenti π era 3,14. Non c'era alcuna norma per scegliere quale π utilizzare. Si rimane con l'impressione che l'opera innovativa di Liu e Tsu fosse ignorata dai matematici che vissero dopo di loro."
Ma la storia del pi greco non finisce certo qui!
Nel 1593 François Viète (1540-1603) trovò una splendida rappresentazione del pi greco attraverso un prodotto infinito:
Il secondo membro a destra va inteso alla stregua del seguente limite:

dove ∏ è il simbolo di produttoria, che in tal caso implica un prodotto infinito.
Il termine limite an è invece dato dalla seguente formula ricorsiva:

il cui valore iniziale è ovviamente:

Sfruttando tale prodotto infinito, Viète arrivò a calcolare 9 cifre decimali del pi greco.
3 anni dopo, nel 1596, il matematico e maestro di scherma tedesco Ludolph van Ceulen prese in considerazione un superpoligono di ben
.gif)
per calcolare pi greco sino a 20 cifre decimali.
Il pamphlet per mezzo del quale comunicò il suo straordinario risultato termina con le parole: "chiunque lo voglia, può avvicinarsi ancora di più", e nessuno lo desiderava più di lui stesso.
Non gettò mai la spugna e continuò a calcolare π fino a 32 e poi 35 cifre decimali, che furono persino incise sulla sua lapide!
Ritornando ai prodotti infiniti, nel 1655 John Wallis scoprì che:
Proseguendo il lavoro di Wallis, Lord William Brouncker (1620-1684) determinò questa magnifica "frazione continua":
Nel 1671 James Gregory e poi, nel 1674, Leibniz scoprirono (cioè riscoprirono la cosiddetta serie delle arcotangenti, la quale pare fosse stata effettivamente scoperta dall'indiano Madhava di Sangamagrama (1350-1425)) che:
Successivamente, nel 1699, l'astronomo Abraham Sharp arrivò a determinare ben 71 decimali corretti, stracciando dunque il record di Van Ceulen, che era arrivato a 35.
Per compiere tale impresa, Sharp sfruttò la seguente serie, chiamata nientemeno che serie di Sharp:
Ma così come nelle competizioni olimpiche, i record non rimangono eternamente gli stessi.
Infatti, già nel 1706 l'ottimo risultato di Sharp venne oltrepassato dall'inglese John Machin, il quale rinvenne 100 cifre sfruttando la formula:
A sua volta Machin venne battuto nel 1717 dal francese Thomas de Lagny, che ne aggiunse altre 27.
Nel 1748 Eulero pubblicò la già citata introductio in analysis infinitorum, ove riportò una carrellata di serie relative al pi greco, come queste:
Nel 1761 avvenne un evento fondamentale nella storia del pi greco.
Infatti, il matematico svizzero Johann Heinrich Lambert (1728-1777) inviò all'Accademia di Berlino la dimostrazione del fatto che il numero π è irrazionale.
A dir la verità, Lambert ottenne un risultato ancor più generale, dimostrando infatti che se x è un numero razionale diverso da 0, allora la sua tangente (tan x) non può essere razionale.
Giacché
.gif)
e 1 è senza dubbio un numero razionale, ne deriva che il numero π/4 non può essere razionale.
Ergo, anche π non è razionale!
Come già affermato, pi greco è dappertutto, pure nel calcolo delle probabilità.
A proposito di calcolo delle probabilità, nel 1777 il matematico francese George-Louis Leclerc, conte di Buffon (1707-1788) propose e risolse una spinosa questione nota (non a caso) come "problema dell'ago di Buffon".
Il problema è questo: innanzitutto bisogna porre sul pavimento un grande foglio di carta, con le righe parallele situate a una distanza fissa d.
Dopodiché è necessario prendere un ago corto di lunghezza l.
Inoltre deve sussistere la relazione:
.gif)
L'interrogativo che ne scaturisce è: qual è la probabilità che l'ago si fermi in modo tale da intersecare una delle righe?

Ebbene, tale probabilità è uguale a:
.gif)
Nel caso particolare in cui la distanza tra le righe è eguale alla lunghezza dell'ago, ne deriva che tale probabilità diviene ovviamente:
.gif)
Perciò si potrebbe, in teoria, determinare il valore di π gettando più volte l'ago su un foglio e calcolando il rapporto tra i lanci e le occasioni in cui l'ago intercetta la riga.
Un test di questo genere venne eseguito dal matematico Mario Lazzarini nel 1901.
Sembra che egli costruì una macchina apposita per lasciar cadere un bastoncino su un foglio ben 3408 volte!
Ebbene, il bastoncino incrociò una delle righe 1808 volte.
Tenendo presente che nel suddetto test il rapporto
.gif)
Lazzarini pervenne a questo valore di pi greco:
il quale è incredibilmente corretto sino a 6 cifre decimali (per via del trucchetto delle lunghezze utilizzato da Lazzarini: guardate qui)!
Nel 1794 lo sloveno Jurij Vega arrivò a calcolare 140 cifre decimali di pi greco, di cui 136 corrette.
Nel medesimo anno, Adrien-Marie Legendre dimostrò che π² è irrazionale e, allo stesso tempo, ipotizzò che esso fosse anche trascendente (ovvero non è algebrico, ossia non è soluzione di alcuna equazione di carattere polinomiale a coefficienti razionali).
Nel 1844 il matematico tedesco (famoso per la sua incredibile abilità nel calcolo mentale) Johann Martin Zacharian Dase riuscì a portare il record di cifre di pi greco calcolate a 200.
Ma Dase non ebbe molto tempo per vantarsi visto che nel 1853 l'inglese William Rutherford pervenne allo straordinario calcolo di 440 cifre decimali!
Quest'ultimo avrebbe poi incoraggiato il suo protetto, William Shanks, un matematico dilettante che gestiva un collegio a County Durham, a spingersi oltre.
Infatti, egli calcolò ben 707 cifre, di cui, tuttavia, solamente 527 corrette.
Se volete saperne di più su Shanks, vi invito a leggere l'interessante post di Paolo Alessandrini "William Shanks, ovvero il calcolatore umano", sul blog Mr. Palomar.
Il 1882 rappresenta un'altra data importantissima in questa storia: nel suddetto anno il matematico tedesco Carl Ferdinand Lindemann (1852-1939) pubblicò un articolo intitolato "Sul numero π", nel quale dimostrò che il numero π non può essere algebrico ed è invece trascendente.
Lindemann giunse a tale conclusione mostrando che la famosa equazione di Eulero
.gif)
non poteva essere soddisfatta da nessun numero x, nel caso in cui x fosse algebrico.
Poiché il numero π soddisfa l'equazione non può essere algebrico: è trascendente!
Ritornando ai matematici alle prese con le cifre decimali del pi greco, durante la Seconda guerra mondiale D.F. Ferguson si mise a calcolare a mano pi greco.
A maggio del 1945 era a 530 cifre e, nel luglio dell'anno successivo, arrivò addirittura a 620: nessuno ha mai calcolato più cifre facendo uso di solo carta e penna.
Negli anni successivi, Ferguson continuò la sua ricerca delle cifre con l'aiuto di una calcolatrice da tavolo, giungendo ad ottenerne 808.
Nel settembre del 1949 John von Neumann, George Rietwiesner e Nicholas Constantine Metropolis sfruttarono l'Electronic Numerical Integrator and Computer (ENIAC) per pervenire, dopo un lasso di tempo di 70 ore, al rinvenimento di un numero di cifre assolutamente straordinario: 2037.
 |
| John von Neumann |
Da questo momento in poi tale spasmodica ricerca delle cifre del pi greco continuò soltanto grazie al supporto informatico.
Ad esempio, nel 1954 la marina statunitense trovò 3089 cifre in 13 minuti sfruttando il supercomputer NORC.
Nel frattempo, i matematici non si son fermati sul fronte delle serie.
Il genio indiano Srinivasa Ramanujan (1887-1920), nel 1910, elaborò una meravigliosa formula inerente al pi greco:
Tale formula converge verso pi greco a una velocità strabiliante.
Se volete saperne di più sull'incredibile Ramanujan, vi consiglio questo splendido post del giovane Marco Cameriero.
Ispirati da Ramanujan, nel 1987 i matematici di origine ucraina Gregory e David Chudnovsky sono riusciti nell'incredibile impresa di elaborare una formula ancor più straordinaria di quella di Ramanujan stesso:
Praticamente, ogni nuovo termine di questa serie aggiunge circa 15 cifre decimali esatte di π!
Una decina di anni dopo, nel 1996, David Bailey, Peter Borwein e Simon Plouffe introdussero una formula senza precedenti:
Perché è così straordinaria?
Il motivo risiede nel fatto che essa consente di calcolare una specifica cifra di pi greco senza calcolare le cifre precedenti!
Sussiste un però: le cifre non sono decimali, bensì esadecimali (cioè in base 16), a partire dalle quali si possono ricavare cifre in base 8 (ottali), 4 (quaternarie) o 2 (binarie).
Nel 1998 il programmatore francese Fabrice Bellard sfruttò questa serie per mostrare che la centomiliardesima cifra esadecimale di π è 9.
Un paio di anni dopo si era arrivati a 250 milioni di milioni di cifre esadecimali!
Lo stesso Bellard, nel dicembre del 2009, rinvenne la bellezza di quasi 2,7 trilioni (un trilione è 10 elevato alla 18) di cifre decimali di pi greco: un record!
Record oltrepassato ancora: l'attuale record è quello detenuto, a partire dal 2011, da Alexander J. Yee e Shigeru Kondo, ovvero 10 trilioni di cifre decimali!
La nostra storia (ovviamente non completa ed esaustiva) del pi greco termina qui, ma sicuramente, in futuro, verranno effettuate nuove scoperte concernenti questo superlativo numero e saranno rinvenute sue nuove cifre.
Vi lascio con il seguente eccezionale video (il cui sottofondo è rappresentato dal celeberrimo brano ragtime The Entertainer di Scott Joplin).
---------------------------------------------------------------------------------------
Fonti principali:
- Viva la scienza di Antonio Mingote e José Manuel Sánchez Ron
- C'era una volta un numero di George Gheverghese Joseph
- Il meraviglioso mondo dei numeri di Alex Bellos
- La piccola bottega delle curiosità matematiche del Professor Stewart di Ian Stewart
- Il mistero dell'alef di Amir D. Aczel
- http://it.wikipedia.org/wiki/Pi_greco#Storia


.gif)
.jpeg)

.gif)
.gif)
.gif)
.gif)
.gif)
.gif)

.gif)
.gif)
.gif)
.gif)
.gif)




.gif)
.gif)
.gif)
.gif)
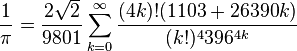





















Post come sempre mooolto dettagliato. Un'ottima risorsa da mettere tra i preferiti per avere sempre a disposizione notizie sulla storia del Pi greco.
RispondiEliminaMolte delle tappe del Pi greco le conoscevo avendone lette qua e là, ma vederle qui tutte insieme fa un certo effetto. Certo, è impossibile raccogliere tutta la storia del Pi greco in un unico post, ma tu comunque ci sei andato mooolto vicino.
Complimenti quindi per l'articolone.
Un saluto
PS:
grazie per la menzione al mio Rama (per gli amici)
Grazie 3140/pi!!!!!!!
EliminaEffettivamente, mi son avvicinato (data la lunghezza del post) asintoticamente alla storia completa del pi greco. ;)
In merito al tuo Rama, è veramente ottimo e dunque assolutamente degno di segnalazione!
Un salutone!
Leo
Sono balbuziente: se scrivo è normale che riporti la dizione esatta "Pi greco"; se parlo, ahimè, mi risulta difficile emulare quanto possa scrivere in quanto, verosimilmente, finisco con il pronunciare "P ... P ... P ... Pipì greco".
RispondiEliminaFantastico tale numero, pressoché magico, che nel lontano 1972, sottese la "griglia" della mia tesi di laurea dedicata all'osanna della "Geometria pitagorica".
Grazie
ciao, quello che hai fatto è davvero incredibile molto approfondito e interessante, grazie ciao!
RispondiElimina