Infatti in passato abbiamo per esempio parlato della curva che congiunge 2 punti nel minor tempo possibile (il problema della brachistocrona), della spettacolare elica cilindrica con le sue fondamentali applicazioni nel mondo dell'arte e di curve cubiche come la versiera di Agnesi e la cissoide di Diocle.
In questo post vogliamo però condurre un discorso più generale relativo alle curve (con particolare riferimento a quelle regolari), che ci porterà a illustrare l'importante concetto di integrale curvilineo (detto pure integrale di linea), almeno nella sua prima forma.
Se avete familiarità con la nozione di integrale definito, osserverete che l'integrale di linea è una semplice estensione del concetto inerente al "magico" mondo delle curve.
Ma procediamo per gradi!
Innanzitutto, partiamo dalle fondamenta: che cos'è una curva?
È facile pensare all'idea di una curva, un insieme di punti nello spazio in cui una particella è libera di muoversi con un singolo grado di libertà; leggermente più difficile è fornire una definizione davvero rigorosa dal punto di vista matematico.
Assumendo di riferirci allo spazio vettoriale ℝn, l'analisi matematica ci definisce una curva come una funzione (vettoriale) continua del tipo

dove I è un generico intervallo.
Di solito quando consideriamo I alla stregua di un intervallo chiuso e limitato (ossia compatto per il teorema di Heine-Borel) [a,b], si parla di arco di curva.
Per chi non ricordasse esattamente cosa significa funzione continua, ne diamo 2 definizioni, una che potrebbe comprendere anche un bambino e l'altra per gli amanti del rigore matematico.
Una funzione è continua (in tutti i punti) quando per tracciarla graficamente su un sistema di riferimento cartesiano non è necessario staccare mai la matita dal foglio!
In termini formali invece una funzione si dice continua in un punto x₀ se vale la seguente uguaglianza:

Se tale uguaglianza risulta valida per qualsiasi punto dell'intervallo [a,b] considerato, allora la funzione è continua in tutto l'intervallo.
Detto ciò, si definisce traccia o sostegno γ* della curva γ l'immagine di γ, ossia, in simboli:

Per farsi un'idea più concreta di cosa sia la traccia è sufficiente pensare alla traiettoria di un moto nello spazio e che racchiude in sé gli aspetti geometrici della curva.
Assumiamo ora che una curva (nello spazio euclideo tridimensionale) venga definita da una generica funzione (vettoriale) continua

Tale funzione vettoriale r si chiama parametrizzazione della curva e contiene le informazioni sul modo in cui la curva viene percorsa.
In particolare, si avrà che

ove la variabile t ∈ [a,b] viene detta parametro della curva e i,j,k sono i classici versori relativi agli assi cartesiani.
In sostanza, al variare di t, r(t) descrive γ, che è il sostegno della curva (trattasi semplicemente di una notazione diversa per esprimerlo).
Una stessa curva può essere parametrizzata in infiniti modi diversi.
Diciamo ora che una curva (o un arco) è chiamata semplice se la funzione r(t) risulta iniettiva.
Un arco

si dice chiuso se

Un arco di curva è poi detto chiuso semplice se la funzione è iniettiva e vale la condizione appena scritta.
Resta il fatto che spesso, specialmente in ambito fisico, è utile pensare ad r(t) come ad una funzione descrivente la posizione all'istante t di una particella che si muove nello spazio euclideo tridimensionale.
In sostanza, si sta assumendo un'interpretazione cinematica della nozione di curva.
Le innumerevoli parametrizzazioni della medesima curva rappresentano, da questo punto di vista, gli infiniti modi diversi (con velocità diverse) di percorrere tale traiettoria.
Diciamo, in particolare, che la funzione vettoriale r è derivabile se tali sono le sue componenti scalari.
Avremo naturalmente che la sua velocità (o derivata) è data da:
mentre la velocità scalare è la norma di tale vettore, cioè

Se poi anche r' risultasse a sua volta derivabile, l'accelerazione (vettore) sarebbe fornita ovviamente dalla formula:

La velocità e l'accelerazione vanno, tra le altre cose, a fornire una classificazione dei moti.
Si ha infatti un moto uniforme quando il modulo della velocità risulta costante; in caso contrario si parla di moto vario.
In quest'ultimo caso, se l'accelerazione risulta costante si parla di moto uniformemente accelerato quando sussiste un incremento (nel tempo) del valore assoluto della velocità, mentre si parla di moto uniformemente ritardato (o decelerato) quando la velocità decresce nel tempo.
Tornando alle curve, diciamo finalmente che una curva γ è regolare (o liscia) se essa risulta continua e derivabile nell'intervallo I considerato e se inoltre
Per di più, una curva si dice regolare a tratti (o anche generalmente regolare) se I si può suddividere nell'unione di un numero finito di intervalli su ciascuno dei quali γ è regolare.
Può inoltre capitare che la curva sia contenuta in un piano. In tal caso si dice che la curva è piana.
Nello specifico, è possibile assegnare una curva piana tramite una funzione continua del tipo

Le curve che risultano piane, semplici e chiuse assumono una denominazione specifica: curve di Jordan (da Camille Jordan, matematico francese di cui abbiamo parlato qui).
Un importante teorema della topologia asserisce, in parole povere, che ogni curva di Jordan divide il piano in 2 parti, una "interna" (limitata) ed una "esterna" (illimitata).
Da Wikipedia riporto una bella immagine illustrativa del suddetto teorema della curva di Jordan.
Nel dettaglio, si dirà che il punto

precede il punto

nel verso indotto dal parametro t se

ATTENZIONE: due parametrizzazioni diverse delle stessa curva non è detto che inducano lo stesso orientamento!
È necessario a questo punto andare a definire il fondamentale concetto di lunghezza di una curva.
A tal proposito, sia γ ⊂ ℝ³ una curva avente estremi A e B.
Una poligonale inscritta in γ è semplicemente una spezzata costruita nel modo seguente: dopo aver fissato un numero intero n, si scelgono n punti consecutivi
su γ, si fissa un punto iniziale ed un punto finale, e si congiunge ciascun punto con il successivo attraverso un segmento di linea retta, come illustrato nella figura di cui sotto.
La lunghezza della spezzata sarà quindi in generale:
La lunghezza L di una curva rappresenta perciò l'estremo superiore delle lunghezze delle poligonali inscritte.
In particolare, se L < +∞ si dice che la curva è rettificabile.
Naturalmente, se la curva presenta una lunghezza infinita essa risulta non rettificabile.
Il problema della suddetta definizione di lunghezza sta nel fatto che è un po' scomoda operativamente.
Il nostro obiettivo sarà quello di passare ad una formulazione della lunghezza di una curva sotto forma di integrale.
A tal proposito, denotiamo con

una parametrizzazione di γ.
I punti Pk della poligonale corrispondono a dei valori tk del parametro.
Si può pertanto scrivere:
Nell'ultima sommatoria è possibile riconoscere le norme dei rapporti incrementali di r(t).
Se supponiamo che la funzione r sia continua e derivabile (ovvero che ciascuna sua componente lo sia), ci si può ricondurre ad una somma di Riemann della funzione ||r'(t)||.
Ne consegue che se abbiamo una curva regolare semplice γ con parametrizzazione fornita dal vettore r(t), la lunghezza di tale (arco di) curva viene fornita dall'integrale:

Si noti bene che la lunghezza così ottenuta è indipendente dalla parametrizzazione scelta!
Vediamo subito un semplice esempio.
Si consideri l'elica cilindrica di equazione vettoriale
Per determinare la lunghezza di questa elica, la prima cosa da fare è andare a derivare il nostro vettore r, per ricavare il vettore velocità:
A questo punto a noi interessa determinare la norma del vettore velocità (basta fare la radice quadrata della somma dei componenti elevati al quadrato), dunque:
Se ricordate l'identità fondamentale della trigonometria

il tutto si riduce semplicemente a:
A questo punto basta immettere quanto trovato nella formula dell'integrale che ci permette di determinare la lunghezza:
Prima di procedere all'introduzione del concetto di integrale curvilineo di prima specie, è necessario specificare che spesso quanto appena illustrato viene espresso in termini della cosiddetta ascissa curvilinea (o parametro arco).
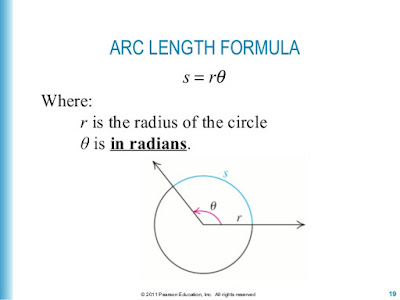
Il modo più semplice per definire questo concetto è nell'ambito delle circonferenze.
Sappiamo bene che la lunghezza di una circonferenza è 2π r, ove r è il raggio della circonferenza.
Sappiamo altrettanto bene che all'intera circonferenza corrisponde un angolo al centro di 360°, ovvero di 2π.
Immaginiamo ora di considerare un arco, che denotiamo con s, di questa circonferenza.
Ad esso è sotteso un generico angolo φ.
Possiamo a questo punto impostare una semplice proporzione:

da cui si ricava:

In ambito fisico, in particolare, questa ascissa curvilinea s, così come l'angolo sotteso all'arco, saranno dipendenti dal tempo t e dunque si scriverà:

Questo è il modo di esprimere la legge oraria di una particella in moto circolare attraverso l'ascissa curvilinea.
Allargando il discorso alle curve in generale, l'ascissa curvilinea è una riparametrizzazione particolare di una curva ottenuta fissando l'estremo di integrazione a in maniera tale che l'integrale

dipenda unicamente dall'estremo superiore t inteso come variabile.
Pertanto s designa, in parole povere, la lunghezza dell'arco di curva a partire da un punto fisso a.
In particolare, possiamo esprimere il vettore velocità in termini di ascissa curvilinea nel seguente modo

assumendo naturalmente che la curva sia regolare e dunque il modulo della velocità non sia mai nullo.
Ricordo che la notazione del punto sopra la lettera s serve ad indicare la derivata prima fatta rispetto al tempo.
Il versore denotato con la lettera greca tau prende la denominazione di versore tangente e si può ovviamente esprimere attraverso la seguente formula:
Ed eccoci finalmente al nocciolo della questione: l'integrale curvilineo di prima specie, detto anche integrale curvilineo riferito all'ascissa curvilinea.
Sia

una funzione continua definita in un sottoinsieme A di ℝn e sia γ una curva regolare parametrizzata da

L'integrale di linea di prima specie di f lungo γ sarà dato da:
Considerando lo spazio euclideo tridimensionale, questa espressione può essere scritta in modo più esplicito come:
Vediamo un primo esempio di calcolo di un integrale di linea.

dove
La nostra curva è sostanzialmente la semicirconferenza nel piano xy centrata nell'origine, avente raggio 2 e posizionata sopra l'asse delle x.
Il problema ora è, data questa curva, arrivare a una parametrizzazione che ci consenta di procedere con il calcolo dell'integrale.
Cosa si può fare?
È molto semplice! Andiamo a porre:
in questo modo, andando a sostituire tutto ciò all'interno dell'equazione della curva, avremo:


cioè

Dunque possiamo scrivere
ovvero esprimere la parametrizzazione (sicuramente regolare) come:
L'intervallo di variazione del parametro t sarà dato da [0, π], dato che ci stiamo riferendo a una semicirconferenza sopra l'asse delle x.
Andiamo a questo punto a derivare questa espressione, ottenendo:

Il calcolo della norma di tale vettore è semplicissimo e restituisce

Siamo ora in possesso di tutti gli elementi necessari per procedere al calcolo dell'integrale curvilineo:
Ho omesso i semplici passaggi dell'ultimo calcolo (è sufficiente sfruttare il metodo di sostituzione ponendo u = cos t).
Vediamo un secondo esempio:

ove γ è l'arco dell'ellisse

contenuta nel primo quadrante.
Come visto nell'esempio precedente, la primissima cosa da fare è andare a parametrizzare la curva.
Il metodo è il medesimo e restituisce la seguente parametrizzazione:

Per quanto concerne l'intervallo di variazione del parametro t, esso è [0, π/2] in quanto stiamo considerando la parte di ellisse contenuta unicamente nel primo quadrante del piano cartesiano.
Come in precedenza, si deriva l'espressione e poi si procede al calcolo della norma.
Nel suddetto caso si ottiene:
Risulta conveniente sfruttare la relazione fondamentale della trigonometria

riscrivendo il seno come
e dunque la nostra norma diventa:Andiamo dunque ad impostare il nostro integrale di linea:
Anche in tal caso è conveniente far uso del metodo di sostituzione.
Quando abbiamo a che fare con l'integrale di una certa funzione sotto radice quadrata e fuori dall'integrale c'è una quantità che potrebbe essere la derivata della funzione argomento della radice, la cosa da fare è andare a porre un parametro generico uguale a tutto l'argomento della radice!
Nel nostro caso bisogna quindi porre
dopodiché si va derivare l'espressione ricavando il differenziale du, da cui poi è semplice trovare il differenziale dt che deve essere sostituito nel nostro integrale.
Vedrete immediatamente che, procedendo in tal maniera, l'espressione dentro l'integrale al di fuori della radice si semplifica, rendendo così agevolissimo il calcolo dell'integrale nella variabile u.
Il tutto si riduce infatti, alla fine, a:
Elenchiamo ora alcune proprietà fondamentali dell'integrale curvilineo di prima specie.
Consideriamo a tal proposito una curva regolare a tratti γ e due funzioni continue

Abbiamo che:
1)
ovvero la proprietà di linearità rispetto all'integranda.
2)

Tale uguaglianza ci dice, in parole povere, che l'integrale di linea risulta indipendente, oltre che dalla parametrizzazione della curva, anche dalla sua orientazione.

dove L è naturalmente la lunghezza della curva.
4)
Se si assume che f ≥ 0, all'integrale di linea si può inoltre fornire una rilevante interpretazione geometrica.
Sia γ una curva piana, regolare a tratti, di equazione
La curva Γ di equazione
è contenuta nel grafico di f.
Al variare di t dall'estremo a all'estremo b, il segmento di retta parallelo all'asse z di estremi r(t) ed R(t) va a descrivere una superficie, che denotiamo con S.
Il prodotto

può essere interpretato come l'area di un rettangolo avente base ds e altezza f(r(t)).
Ergo, l'integrale

può esser visto geometricamente come area della superficie S.
In conclusione, deliziamoci con un ottimo passo, inerente alla storia dello sviluppo del concetto di curva, tratto dal libro La forma delle cose di Marco Andreatta:
"Nel '600 due grandi matematici francesi, René Descartes (1596-1650) e Pierre de Fermat (1601-1665), rivoluzionano la teoria dello studio delle curve e, di conseguenza, quello della geometria. Non è facile attribuire la paternità delle tante scoperte e dei nuovi metodi all'uno o all'altro; su questo furono essi stessi protagonisti di una disputa feroce, descritta in tanti libri di storia della matematica...Cartesio, nel solco della tradizione greca, vuole risolvere problemi matematici con l'uso delle curve, dividendoli in 3 classi. La prima è quella dei problemi risolubile con riga e compasso. La seconda, la più interessante, raccoglie tutti i problemi che possono essere risolti da curve tracciabili con un singolo moto, o alternativamente con l'uso di nuovi compassi; chiama queste curve ammissibili o geometriche. Nella terza classe mette i problemi che non stanno nelle prime due e chiama queste curve immaginarie o meccaniche, tra cui la quadratrice e la spirale.
Cartesio dedica molto tempo alla costruzione effettiva di nuovi compassi; tra questi il trisettore, che disegna una curva che triseca un angolo...Il lume individuato da Cartesio è l'idea di pensare una curva nel piano attraverso un'equazione, dando origine con questo a quella che oggi viene definita geometria analitica o geometria algebrica...Cartesio propone che una curva nel piano sia determinata, fissato un sistema di riferimento, dai punti le cui coordinate cartesiane (x,y) soddisfano un'equazione f(x,y) = 0, dove f(x,y) è una funzione nelle variabili x e y...Si osservi che quando Cartesio parla di funzioni intende sicuramente funzioni esprimibili come polinomi; inoltre le curve che chiamava in una prima fase geometriche, ovvero costruibili con i nuovi compassi, sono di fatto curve algebriche, come provato da Kempe...Non tutti le funzioni sono polinomiali, si pensi ad esempio alla funzione esponenziale o alle funzioni trigonometriche; queste funzioni, dette anche trascendenti, nascono pochi anni dopo Cartesio nei lavori di Leibniz, Newton e tanti altri che creano il calcolo differenziale e integrale...In alcuni casi, attraverso opportuni passaggi algebrici, è possibile ricavare dall'equazione f(x,y) = 0 una delle due variabili come funzione rispetto all'altra...In questo caso si dirà che la curva è descritta come grafico (della variabile dipendente in funzione di quella che varia liberamente).
La descrizione di una curva come grafico è molto utile, ma è possibile solo sotto certe condizioni di regolarità, studiate in un celebre risultato dal matematico italiano Ulisse Dini (1845-1918): la curva è un grafico in un intorno dei suoi punti non singolari.
La definizione di curva come luogo degli zeri di una funzione può essere ricondotta a quella greca di termine o bordo di una superficie.
Se invece si pensa a una curva come a un insieme di punti o monadi, equivalentemente a un punto in movimento, si descrive la curva come i punti del piano cartesiano le cui coordinate (x(t), y(t)) sono descritte da funzioni x(t) e y(t), al variare di un parametro continuo t. Queste equazioni si dicono equazioni parametriche della curva...Nella Geometria Cartesio dimostra, tra tanti altri risultati, il fatto abbastanza stupefacente che le curve di grado 2 sono tutte e solo le coniche (con l'avvertenza di chiamare coniche degeneri anche le unioni di due rette). La geometria greca delle coniche si ingloba dunque in questa teoria più generale; lo studio delle coniche si riduce semplicemente allo studio dei polinomi in due variabili di grado 2.
Cartesio si avventura quindi nello studio delle curve di ordine superiore, riconsiderando con la sua definizione molti esempi classici e creandone di nuovi.
Tra questi il Folium (foglia), la cui equazione cartesiana è

mentre quella parametrica è
Cartesio sbagliò a disegnare questa foglia, convinto che si ripetesse uguale nei quattro quadranti; probabilmente anche per la poca dimistichezza con i numeri negativi. Il primo a disegnare correttamente il Folium fu Christiaan Huygens.
Il Folium di Cartesio è una curva di grado 3, una cubica, che presenta una novità rispetto alle curve di grado 1 (rette) e di grado 2 (coniche): ha un punto singolare.
Pensare alle curve come luogo di zeri di un'equazione introduce l'uso dell'algebra nello studio della geometria, chiarendo e risolvendo in maniera estremamente efficace e rigorosa molti problemi; tra questi la questione delle rette tangenti e dei punti singolari.
Questo rivoluzionario modo di affrontare la geometria si impone rapidamente e ha raggiunto oggi livelli di raffinatezza e astrazione sorprendenti...Le novità introdotte da Cartesio sono naturali conseguenze delle nuove tecniche algebriche per la ricerca delle radici di un polinomio, condotte con successo nel '500 da italiani quali Cardano, Tartaglia, Scipione Dal Ferro e Ferrari."
Nel prossimo appuntamento andremo a scoprire gli integrali curvilinei di seconda specie, le forme differenziali lineari e la teoria del potenziale.
-----------------------------------------------------------------------------------------
Fonti essenziali:
- Analisi matematica 2 di Carlo Domenico Pagani e Sandro Salsa
- Analisi matematica vol. 2 di Barutello, Conti, Ferrario, Terracini, Verzini
- Analisi matematica due di Fusco, Marcellini e Sbordone
- La forma delle cose di Marco Andreatta















































Nessun commento:
Posta un commento