Andremo a scoprire 2 particolari curve cubiche, simili fra loro: la versiera di Agnesi e la cissoide di Diocle.
La versiera di Agnesi è una particolare curva cubica piana attribuita alla matematica italiana Maria Gaetana Agnesi (1718-1799) nell'opera in 2 volumi, datata 1748, Istituzioni Analitiche ad uso della gioventù italiana.
Trattasi del primo manuale completo che prende in esame sia il calcolo differenziale che quello integrale, oltre ad essere il primo libro di matematica a noi pervenuto scritto da una donna e pure uno dei primi contributi concernenti la geometria analitica provenienti dall'Italia.
In una nota, il Consiglio dell'Accademia delle Scienze di Parigi riferisce:
"Fu necessaria molta abilità e furbizia per ridurre, come ha fatto l'autrice, a un metodo quasi uniforme queste scoperte sparse tra le parole dei matematici moderni e spesso presentate con metodi molto differenti tra loro. Ordine, chiarezza e precisione regnano in tutte le parti di quest'opera."
Nata a Milano il 16 maggio 1718, terza di 21 fratelli, bambina prodigio, Maria Agnesi a 13 anni parlava almeno 7 lingue (l'italiano, il tedesco, il francese, il latino, il greco, lo spagnolo e l'ebraico), al punto che venne soprannominata Oracolo settelingue.
Nel 1737, per non disubbidire ai voleri del padre (facoltoso commerciante di seta), i suoi studi si spostarono dall'ambito delle lingue a quello filosofico e matematico.
Nel frattempo casa Agnesi era diventata uno dei salotti più gettonati di Milano, ove erano soliti recarsi intellettuali italiani e da mezza europa.
Proprio questi introdussero la giovane agli Elementi di Euclide, alla Logica, alla Metafisica e alla Fisica Generale.
Addirittura, era diventata una tradizione la discussione da parte di Maria di svariate tesi filosofiche nel salotto di casa Agnesi, tutte (ben 191) pubblicate nel 1738 in una raccolta intitolata Propositiones Philosophicae.
Tuttavia, per buona parte della sua vita trascurò i rapporti sociali, scegliendo di dedicarsi completamente allo studio della matematica e della religione, al punto che arrivò a chiedere al padre il permesso di diventare suora!
Pieno di sgomento all'idea che la sua bambina più cara lo volesse abbandonare, egli la pregò di cambiare idea.
La ragazza acconsentì di restare con il padre, a patto di poter vivere in uno stato di relativa clausura e di poter recarsi in chiesa quando lo desiderava.
Nel 1740 incominciò un periodo di collaborazione con padre Ramiro Rampinelli, titolare della cattedra di matematica e fisica all'Università di Pavia e pioniere della matematica analitica.
Grazie al supporto di Rampinelli, l'Agnesi studiò il testo dell'abate Reyneau, Analisi dimostrata (1708) e venne incoraggiata nella preparazione della sua opera più importante, appunto le Istituzioni Analitiche.
La grandiosità di quell'opera spinse addirittura papa Benedetto XIV a proporgli la cattedra di matematica all'Università di Bologna.
Tuttavia, la matematica rifiutò e anzi, dopo la morte del padre (nel 1752), si dedicò completamente ad opere di carità.
Casa Agnesi divenne un rifugio per inferme e lei stessa diventò serva e infermiera.
Successivamente, nel 1771, grazie a una donazione del principe don Antonio Tolomeo Trivulzi venne fondato a Milano il Pio Albergo Trivulzio.
Per merito dell'invito del cardinale Giuseppe Pozzobonelli, nel 1783 Maria Gaetana si trasferì al Pio Albergo in qualità di Visitatrice e Direttrice delle Donne, specialmente inferme.
L'Agnesi era diventata a tutti gli effetti una teologa, al punto che lo stesso Pozzobonelli si rivolse a lei al fine di decidere sull'ortodossia di uno scritto relativo a politica e religione.
Lo stesso non si può dire delle opere scientifiche: era molto remissiva a dare giudizi sulle suddette, infatti quando l'Accademia di Torino le propose di esaminare i lavori di Lagrange inerenti al calcolo delle variazioni, la donna si sottrasse, adducendo le sue serie occupazioni.
Per ben 26 anni rimase al Trivulzio, impegnandosi nell'aiuto delle inferme, fino alla morte, avvenuta il 9 gennaio 1799.
Andiamo ora ad osservare la particolare curva che rese celebre l'Agnesi.
C'è da specificare che, in realtà, la versiera era già stata studiata da Fermat nel 1666 e da Guido Grandi nel 1703 in Quadratura circuli et hyperbolae.
Grandi l'aveva denominata curva con (seno) verso, ovvero contrario, nemico.
Nel 1801 John Colson, Lucasian Professor di Matematica all’Università di Cambridge, in una sua traduzione confuse l’originario significato del nome di derivazione latina della curva con quello di “avversaria" (dal francese aversier), "nemica” (versiera appunto), appellativo attribuito generalmente alle streghe.
Ecco perché ancora oggi la suddetta curva è nota come witch of Agnesi ("strega di Agnesi").
Per costruire la versiera, si parte da un cerchio di raggio a e centro C in un riferimento cartesiano Oxy.
Basandoci sulla raffigurazione seguente

possiamo notare che

Viene poi considerata una retta l, la quale è simultaneamente parallela all'asse x e tangente alla circonferenza nel punto B a distanza 2a dal centro degli assi O.
Si considera inoltre un punto della circonferenza, indicato con M, e viene tracciata una linea che congiunge O con M, intersecando la retta l nel punto N.
Infine, è tracciata una retta perpendicolare all'asse x e passante per il punto N.
Viene dunque definita versiera di Agnesi il luogo dei punti P intersezione della parallela a l passante per M e della parallela all'asse y passante per N, al variare del punto M sulla circonferenza.
Ecco un'animazione che rende chiaro quanto appena scritto:

Ma come si ricava l'equazione cartesiana della versiera?
Innanzitutto notiamo dalla costruzione che i triangoli ODM e OBN risultano simili.
Ergo, vale la seguente proporzione

Osserviamo nuovamente la figura. È facile constatare che BN = DP essendo segmenti di uguale lunghezza.
Indicando allora con x tale lunghezza, con y la lunghezza del segmento OD, con 2a il diametro OB, si ha, per il secondo teorema di Euclide, che DM è medio proporzionale tra i segmenti OD e BD.
Dunque
.gif)
da cui:
.gif)
pertanto
.gif)
o equivalentemente:
.gif)
A questo punto la primissima proporzione può essere riscritta come:

da cui si ricava l'equazione cartesiana della versiera:
La versiera è quindi una cubica razionale avente l'asse x come asintoto d'inflessione, in altre parole la curva si avvicina sempre più all'asintoto dopo aver incontrato 2 flessi, che hanno coordinate

La versiera possiede diverse interessanti peculiarità:
- L'area compresa tra la versiera e il suo asintoto è ben 4 volte l'area della circonferenza utilizzata per descriverla, cioè 4πa²;
- Il volume del solido (a forma di fuso) che si ottiene facendo ruotare la versiere attorno al proprio asintoto è pari a 2 volte il volume che si otterrebbe facendo ruotare la circonferenza intorno all'asse x, ovvero 4π²a³
- Il baricentro della curva coincide perfettamente con il centro della cincorferenza utilizzata per descriverla.
Per a = 1/2 l'equazione diviene

che altro non è che la derivata dell'arcotangente!
 |
| Versiere ottenute per diversi valori di a |
La "strega di Agnesi" trova persino applicazioni in fisica (fenomeni di risonanza), ingegneria e statistica (distribuzione di Cauchy).
Intorno al 180 a.C. il matematico greco Diocle di Caristo scoprì una curva assai simile alla versiera di Agnesi.
La denominò cissoide (dal greco kissoeidēs, "a forma di edera", composto di kissos, "edera", e oeidēs, "forma") e la utilizzò per cercare di risolvere il celebre problema di Delo della duplicazione del cubo, cioè l'impresa di costruire un cubo con un volume pari a 2 volte quello di un dato cubo più piccolo.
In pratica, ciò implica che il cubo più grande debba possedere uno spigolo

volte più grande dell'altro.
L'uso che Diocle fece della cissoide e della sua intersezione con una retta risultava corretto, tuttavia non seguiva rigorosamente le regole delle costruzioni geometriche euclidee, le quali consentivano l'utilizzo solo di riga e compasso.
La cissoide si costruisce partendo da 2 curve qualsiasi C₁ e C₂ e da un punto fisso O.
Se P₁ e P₂ sono i 2 punti in cui una retta passante per O interseca C₁ e C₂, si determina sulla retta stessa il punto P tale che OP = P₁P₂.
Il luogo dei punti P è detto cissoide di C₁ e C₂ rispetto al polo O.
La cissoide di Diocle è un caso particolare di cissoide in cui le 2 curve sono rappresentate da un cerchio e una sua tangente, e, inoltre, come punto fisso l'altro estremo del diametro del cerchio nel punto di tangenza.
L'equazione in coordinate cartesiane della cissoide di Diocle è:

o equivalentemente:

La cissoide può anche venir generata dal vertice di una parabola che ruota, senza strisciare, su una seconda parabola di identica grandezza.
Concludiamo il post con 2 video relativi agli argomenti trattati:
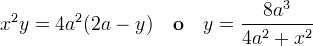










.gif)








Forse sarebbe interessante notare come lo studio della versiera di Agnesi abbia portato Grandi alla conclusione che la serie che da lui prende nome possa convergere a 1/2: http://raffrag.wordpress.com/2014/01/21/mathematicae-disputationes/.
RispondiEliminaGrazie mille dell'interessante segnalazione!!
Elimina