INTEGRALI DEFINITI E DERIVATE PARZIALI: STORIA, PROPRIETÀ E APPLICAZIONI IN FISICA

Tempo fa avevo scritto un articolo inerente al calcolo differenziale e integrale, dal titolo "Derivate e integrali indefiniti: storia, proprietà e applicazioni in fisica"; ora vorrei proseguire la trattazione introducendo gli importanti concetti di integrale definito e derivata parziale.
Iniziamo dagli integrali.
Ricordiamo intanto cos'è un integrale indefinito, in modo da introdurre agevolmente il suo "cugino" definito!
L'integrale indefinito è quel processo che, partendo dalla derivata di una funzione, ci permette di ritornare alla funzione di partenza, o meglio all'insieme di funzioni di partenza, detto insieme delle primitive.
Un semplice esempio:






Traducendo in parole: abbiamo x² rappresentante una derivata; integrando ottieniamo x³/3 + c, ovvero la famiglia delle primitive.
Vi ricordate perché si scrive il risultato con l'aggiunta di c?
Se non lo rimembrate, il motivo sta nel fatto che la derivata (nel nostro esempio x²) non proviene da un'unica funzione di partenza, ma appunto da un insieme infinito di funzioni (le primitive).
Il termine c indica infatti una costante e, come risulta noto, la derivata di una costante è semplicemente 0.
Prima di passare agli integrali definiti, approfondiamo un po' di più quelli indefiniti, introducendo 2 utili tecniche di risoluzione dei suddetti: l'integrazione per parti e l'integrazione per sostituzione.
La prima tecnica ci permette di risolvere integrali come questo:





Tale integrale non si risolve immediatamente, alla stregua del precedente: abbiamo bisogno di integrarlo per parti.
Il processo di integrazione per parti deriva da una regola propria delle derivate: la cosiddetta regola di Liebniz per la derivata del prodotto di 2 funzioni.
Questa regola ci dice che la derivata del prodotto di 2 funzioni si calcola in tal maniera:

Ovviamente è più facile capirla mediante degli esempi.
Come primo esempio consideriamo la funzione f(x) = xsin x.
Ricordiamo innanzitutto che:

• D(x) = 1;
• D(sinx) = cos x.

Applichiamo allora la regola di Leibniz:




Altro esempio: consideriamo la funzione f(x) = 3xcos x.
Ricordiamo che:

• D(3x) = 3;
• D(cos x) = -sin x.

Dunque:





A questo punto riprendiamo la regola di Leibniz generica:

e integriamola ottenendo:

Notiamo che al primo membro troviamo l'integrale di una derivata: ciò è equivalente alla primitiva f(x)g(x).
Pertanto:

Adesso manipoliamo l'espressione:

Quella appena scritta è l'espressione dell'integrazione per parti: essa ci consente quindi di calcolare l'integrale del prodotto di 2 funzioni, una derivata e una primitiva.
Sicché ritorniamo all'integrale che avevamo lasciato in sospeso:





Per calcolarlo possiamo appunto sfruttare l'integrazione per parti.
Osserviamo che:

• f'(x) = e^x;
• f(x) = e^x;
• g(x) = x;
• g'(x) = 1

Tenuto presente ciò, possiamo procedere con l'integrazione per parti:






Un altro esempio:





Prima di procedere per parti, possiamo portare il 2 fuori dall'integrale, in quanto costante:





Riscontriamo che:

• f'(x) = sin x;
• f(x) = -cos x;
• g(x) = x;
• g'(x) = 1.

Procediamo:

Svolgendo i calcoli






Ora scopriamo brevemente l'integrazione per sostituzione.
Partiamo da un esempio:





Integrare per sostituzione vuol dire, in termini semplici, sostituire un'espressione con un'altra più congeniale.
Nel suddetto caso poniamo 1 + x² = t.
Da tale espressione ricaviamo poi la x:




Con una regola che illustreremo adesso, calcoliamo la derivata della radice quadrata di t -1.
Come procediamo?
Siccome la sopracitata funzione è composta, utilizziamo la cosiddetta regola della catena.
In accordo con tale regola, calcoliamo innanzitutto la derivata di ciò che c'è dentro la radice, ossia il suo argomento.
Scriviamo:




Dopodiché, andiamo a considerare la radice quadrata:






La derivata complessiva non sarà altro che il prodotto tra A' e B':

Vi sarete resi conto che, tramite la regola della catena, non abbiamo fatto altro che spezzare la derivazione di una funzione composta in 2 derivazioni più semplici.
Prima di procedere nell'integrazione per sostituzione, evidenziamo che il termine dx che compare alla fine di ogni integrale indefinito si chiama differenziale e rappresenta quella cosa che ci segnala chiaramente rispetto a quale parametro dobbiamo integrare la funzione.
Nell'esempio dato, andremo a sostituire dx con dt, visto che abbiamo effettuato un cambio di variabile!
Dopo queste premesse, procediamo quindi con l'integrazione per sostituzione:

Semplificando otteniamo:

Il risultato è quindi:






Questo però è il risultato per quanto concerne t.
Per tornare ad x, basta aver presente che t = 1 + x² e dunque abbiamo:

Come abbiamo fatto?
Ricapitoliamo:

1) abbiamo sostituito un'espressione (1 + x²) con un'altra (t);
2) abbiamo ricavato da questa uguaglianza la x;
3) abbiamo calcolato la derivata di ciò che equivale a x, cioé radice quadrata di t-1;
4) abbiamo inserito questi nuovi elementi nell'integrale, accompagnati dal nuovo differenziale dt;
5) abbiamo calcolato l'integrale con le regole note;
6) una volta ottenuto il risultato per la t, abbiamo sostituito per riottenerlo con la x.

Esprimendo il tutto in una formulazione generale: sia f(x) una funzione continua e g(x) una funzione derivabile con derivata continua.

Allora:

Quella appena riportata è la formulazione rigorosa dell'integrazione per sostituzione.
Direi che il nostro approfondimento sugli integrali indefiniti può concludersi qui!
Passiamo (finalmente) agli integrali definiti.
Una domanda spontanea potrebbe essere: perché sono chiamati "definiti"?
Si può rispondere molto semplicemente: poiché, a differenza di quelli indefiniti, gli integrali definiti, in generale, ci conducono ad un numero puro, non ad un insieme di primitive.
Infatti, ci permettono, ad esempio, di calcolare l'area sottesa a una data curva.
Sembrerà strano, ma il concetto di integrale definito possiede radici più antiche rispetto al "cugino" indefinito.
A conferma di ciò, già Eudosso di Cnido (408-355 a.C.) ed Archimede di Siracusa (287-212 a.C.) avevano implementato e utilizzato un metodo, detto di esaustione, simile al processo di integrazione definita, che consiste nel calcolare l'area di una figura piana attraverso la costruzione di una successione di poligoni che approssimano sempre più la suddetta figura.
Interessanti informazioni circa il metodo di esaustione e i suoi protagonisti si possono riscontrare in Storia del Calcolo di Carl Benjamin Boyer:

"Alcune fonti rivelano che [Platone] propose a Eudosso parecchi problemi di stereometria che si rivelarono estremamente significativi in direzione del calcolo. A tal proposito, le dimostrazioni fornite da Eudosso delle proposizioni (affermate ma non dimostrate da Democrito) sui volumi di piramidi e coni, lo condussero alla messa a punto del suo famoso metodo di esaustione....Eudosso dovette ricorrere a una procedura che era già stata elaborata da Antifonte il sofista e, successivamente, da Brisone. Costoro avevano inscritto in un cerchio un poligono regolare e, con successivi raddoppi del numero dei lati, ritenevano di pervenire a un poligono coincidente con il cerchio e di determinare, così, l'area ricercata. Non conosciamo le parole esatte (gli scritti) di Antifonte e di Brisone. Il metodo di Antifonte è stato descritto come equivalente sia a quello di Eudosso, sia alla nostra moderna idea del cerchio come limite del poligono inscritto (sebbene espresso con una diversa terminologia). Ma tutto ciò non sembra corretto. Infatti, se Antifonte avesse considerato il processo di bisezione attraverso una successione infinita di passaggi, non avrebbe adottato un modo di pensare compatibile con quello di Eudosso e di Euclide. D'altra parte, non aveva certamente la nostra concezione di limite perché non intese il suddetto processo di bisezione come continuato indefinitamente, ma solo come realizzato fino al grado di approssimazione desiderato. Inoltre, la nostra concezione di limite è numerica, mentre le teorie di Antifonte e di Eudosso sono meramente geometriche. La suggestiva ipotesi di Antifonte fu comunque adottata da Brisone che sembra non si sia limitato a inscrivere un poligono in un cerchio, ma abbia anche circoscritto un altro poligono allo stesso cerchio, sicché la circonferenza sarebbe stata determinata, come il risultato di una prolungata bisezione, dalla progressiva approssimazione dei poligoni inscritti e circoscritti. Anche in questo caso non abbiamo elementi sufficienti per stabilire con certezza quali fossero le effettive tesi avanzate. Si è ipotizzato che contenessero concetti in qualche misura rapportabili alle sezioni di Dedekind o alla teoria del continuo di Cantor, ma in realtà non vi sono sufficienti garanzie per avvalorare una tale interpretazione. Comunque, tali concezioni furono poi sviluppate da Eudosso con argomentazioni rigorose....La procedura di Eudosso divenne nota come metodo di esaustione. Il principio su cui questo metodo è basato viene definito lemma o postulato di Archimede, anche se lo stesso matematico siracusano lo attribuì a Eudosso e non è neanche improbabile che sia stato formulato ancora prima da Ippocrate di Chio. L'assioma afferma che, date 2 grandezze diverse (non nulle, naturalmente, perché lo 0 per i greci non era né un numero né una grandezza), "se dalla maggiore si sottrae una grandezza più grande della sua metà e, da ciò che risulta, una grandezza ancora maggiore della sua metà e se questo processo viene ripetuto infinite volte, ci sarà una grandezza minore della più piccola grandezza che si possa pensare". Questa definizione (in cui, ovviamente, un qualunque numero razionale può esser sostituito in luogo di 1/2) escluse l'infinitesimo da tutte le dimostrazioni della geometria greca, sebbene tale nozione si trovasse occasionalmente in alcune elaborazioni come strumento euristico. Il fatto che, continuando la procedura indicata nell'assioma di Archimede, si possa ottenere una grandezza piccola a piacere, portò a chiamare il procedimento di Eudosso (ma molto più tardi) con il termine di "metodo di esaustione". Il termine "esaustione" non fu utilizzato fino al XVII secolo, quando alcuni matematici, in modo un po' ambiguo e acritico, lo introdussero sia in riferimento all'antica procedura greca, sia ai loro più moderni metodi che conducevano direttamente al calcolo e che hanno veramente "esautorato" le grandezze."   

Come abbiamo appena riscontrato dalla splendida trattazione di Boyer, il metodo di esaustione può essere considerato solamente un'approssimazione delle moderne tecniche relative al calcolo dell'area.
Il tutto dipende soprattutto dalla mancanza, nella matematica greca, del concetto di limite, ossia la nozione basilare dell'analisi matematica, da cui discendono derivate e integrali.
Come anticipato in precedenza, l'integrale definito ci consente di calcolare l'area sottesa ad una curva.
Osservate attentamente la seguente immagine:

Possiamo constatare che l'area sottesa a tale funzione può essere approssimata abbastanza bene dalla somma dei rettangolini rappresentati.
Se incrementassimo il numero n di rettangolini (ovviamente ciascuno di essi si restringerebbe maggiormente) avremmo un'approssimazione dell'area ancora più precisa.
La nostra misura più precisa in assoluto, l'integrale definito, è allora il limite per n tendente all'infinito della sommatoria degli n rettangolini nell'intervallo [a,b].
Possiamo indicarlo così:






Esso si legge: "integrale definito tra a e b di f(x) in dx".
Come già detto, l'integrale definito di una funzione restituisce come risultato un numero puro.
La questione è: come facciamo a calcolare l'integrale definito di una certa funzione?
Il primo suggerimento è: tenere presente tutte le regole concernenti l'integrale indefinito.
Infatti, quando ci troviamo di fronte ad un integrale definito da calcolare, la prima cosa da fare è calcolarlo come se fosse un "semplice" integrale indefinito.
Consideriamo un esempio banale:






Se lo considerassimo alla stregua di un integrale indefinito, trascurando pertanto quei numeretti (2 e 1) agli estremi del simbolo ∫ (introdotto per la prima volta nel 1675 da Leibniz, sostituendolo all'abbreviazione omn), il risultato sarebbe:





Quei numeretti avranno un loro scopo no? O sono stati inseriti dai matematici solo per farci confondere le idee?
L'opzione corretta è ovviamente la prima: essi ci servono per calcolare l'integrale definito.
Essi rappresentano gli estremi dell'intervallo entro il quale andiamo a considerare l'area sottesa ad una data curva (in tal caso f(x) = x² + 3).
Come dobbiamo procedere quindi?
È semplicissimo: dobbiamo sostituire quei valori (2 e 1) alla x dell'espressione ottenuta mediante l'integrazione indefinita e poi dobbiamo sottrarre i suddetti valori.
È più facile a farsi che a dirsi!
Facciamolo allora:






Svolgendo questi calcoli elementari otteniamo il risultato: 16/3.
Adesso un esempio più complicato, ove è necessario sfruttare pure l'integrazione per parti:






Calcoliamolo innanzitutto alla stregua di un integrale indefinito, effettuando l'integrazione per parti.
Osserviamo che:

• f'(x) = e^x;
• f(x) = e^x;
• g(x) = x³;
• g'(x) = 3x².

Procediamo:





Purtroppo ci troviamo nuovamente di fronte ad un'espressione non calcolabile immediatamente.
Per tali ragioni, integriamo per parti l'integrale il cui argomento è x²e^x:

Ci troviamo di nuovo di fronte all'integrale che abbiamo calcolato agli inizi dell'articolo:





A questo punto sostituiamo all'indietro:

Svolgendo i calcoli:

Passiamo all'integrale definito:

Ecco l'immagine rappresentante l'area sottesa alla funzione che abbiamo appena calcolato:











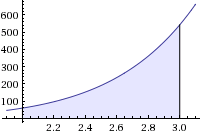
Ma l'integrale definito si applica in fisica?
Certamente!
Illustriamo un semplice esempio.
Avete presente il teorema dell'impulso (di cui abbiamo parlato nell'articolo "La fisica in montagna (e non solo!)")?
Adesso lo andremo a esprimere in modo più rigosoro attraverso l'integrale definito.
Prendiamo una particella (corpo unidimensionale) in un sistema inerziale (in cui vale il 1° principio della dinamica newtoniana) soggetta ad una forza F per un certo periodo di tempo t.
Allora l'impulso impartito dalla forza alla particella è:






Il concetto di impulso è particolarmente utile quando si ha a che fare con forze intense che agiscono su tempi brevi.
Ciò accade, ad esempio, nelle collisioni fra 2 particelle, nella percussione di un chiodo con un martello, ecc.
Tali forze sono denominate impulsive e la loro caratteristica fondamentale è rappresentata dalla dipendenza esplicita dal tempo.
Per capire come una forza impulsiva vada a modificare lo stato di moto di una particella, possiamo scrivere l'impulso impartito in un tempo infinitesimo, sfruttando la seconda legge della dinamica:





Osserviamo che i dt si elidono, lasciando spazio alla quantità mdv.
Ma mdv = d(mv).
Come noto, la grandezza




è la quantità di moto (o momento lineare) della particella al tempo t.
Sapendo questo, possiamo scrivere l'impulso infinitesimo come:




Pertanto, l'impulso sarà:

Ergo, tramite il calcolo differenziale e integrale, abbiamo compreso che l'impulso impartito dalla forza ad una particella comporta una variazione della sua quantità di moto!
Questo era solo un piccolo assaggio delle applicazioni degli integrali definiti alla fisica: ne sussistono innumerevoli!
Passiamo ora a tutt'altra questione: le derivate parziali.
Una domanda spontanea potrebbe essere: cosa le differenzia dalle derivate ordinarie e per quale ragione vengono definite con l'appellativo "parziali"?
1° punto importante: le derivate parziali riguardano funzioni di più variabili reali!
Nel calcolo delle suddette, infatti, non si ha a che fare con funzioni come f(x) = x + 3, dove è presente un'unica variabile indipendente, bensì ci si trova di fronte a funzioni alla stregua di f(x; y) = x + 2y, in cui appaiono 2 variabili indipendenti o anche più.
Nella nostra trattazione, prenderemo come riferimento solo funzioni di 2 variabili reali.
Dunque, dovrebbe essere chiaro che il nominativo "parziali" si riferisce al fatto che deriviamo parzialmente rispetto a una variabile, ad esempio x, ma c'è anche il parametro y nella nostra funzione.
Da cosa cominciamo allora per introdurre in dettaglio le derivate parziali?
Partiremo, come nel caso delle derivate ordinarie, dal rapporto incrementale, o meglio dai rapporti incrementali.
Infatti, data una funzione f(x; y) si dice rapporto incrementale parziale di f rispetto a x relativo al punto (x₀; y₀) il rapporto fra l'incremento parziale ∆xf e l'incremento ∆x della variabile x:

Allo stesso modo, definiamo il rapporto incrementale parziale di f rispetto a y relativo sempre al punto (x₀; y₀) come il rapporto tra l'incremento parziale ∆yf e l'incremento ∆y della variabile y:

Stabilito ciò, possiamo andare a definire le derivate parziali.
Si dice derivata parziale della funzione f(x; y) nel punto (x₀; y₀) rispetto alla variabile x il limite, se esiste ed è finito, del rapporto incrementale parziale rispetto a x al tendere a 0 dell'incremento ∆x:

Si chiama derivata parziale della funzione f(x; y) nel punto (x₀; y₀) rispetto alla variabile y il limite, se esiste ed è finito, del rapporto incrementale parziale rispetto a y al tendere a 0 dell'incremento ∆y:

Altri modi per indicare la derivata parziale della funzione f(x; y) rispetto a x sono:

• f'x(x₀; y₀);
• Dfx(x₀; y₀).

Analogamente, ulteriori modalità per designare la derivata parziale di f(x; y) rispetto a y sono:

• f'y(x₀; y₀);
• Dfy(x₀; y₀).

Dopo tutte queste definizioni formali, andiamo a discernere il succo del calcolo delle derivate parziali.
Per derivare una funzione di 2 variabili reali rispetto a una variabile basta derivare rispetto al parametro selezionato e considerare l'altro come una costante.
Il tutto diverrà molto più chiaro dopo aver osservato alcuni esempi.
Prendiamo la funzione f(x; y) = x² + 3y.
La sua derivata parziale rispetto a x sarà:





La sua derivata parziale rispetto a y sarà invece:






Prendiamo un'altra funzione: f(x; y) = 3x²y + 5x² - 2y².
La sua derivata parziale rispetto a x sarà:

 



La sua derivata parziale rispetto a y sarà:

Potremmo adesso calcolare le derivate seconde.
Come si fa?
Innanzitutto prendiamo la derivata parziale di tale funzione rispetto a x, che abbiamo detto essere 6xy + 10x.
La derivazione può seguire 2 strade: o deriviamo nuovamente rispetto ad x, oppure deriviamo rispetto a y.
Eccole entrambe:

L'analogo vale per quanto concerne la derivazione rispetto alla y.
Riprendiamo allora il risultato della prima derivazione rispetto alla y, ovvero 3x² - 4y e compiamo il medesimo procedimento:










Non riscontrate un particolare suggestivo?
Le 2 derivate miste restituiscono il medesimo risultato (6x).
Ebbene, per il teorema di Schwarz, possiamo asserire che risultano uguali le derivate miste delle funzioni elementari e di tutte le funzioni che si ottengono componendo le stesse tramite operazioni algebriche.
Adesso una breve storia delle derivate parziali, sempre ripresa dallo splendido Storia del Calcolo di Boyer:

"Se si ricorda che la rigorizzazione dei concetti di derivata e di differenziale per funzioni di una variabile risale a Bolzano, Cauchy e Weierstrass dobbiamo allora riconoscere che l'estensione di questi concetti a funzioni di più variabili non è stata del tutto immediata e ha richiesto qualche decennio. Il motivo del "ritardo" non sta certamente nel passaggio dal concetto di derivata a quello di derivata parziale. Queste erano state introdotte già nel corso del XVIII secolo, a opera di matematici quali Jakob e Nikolaus Bernoulli e lo stesso Eulero, [assieme alle] prime ricerche sulle equazioni alle derivate parziali...È "già" del 1873, per esempio, il noto teorema di Hermann A. Schwarz sull'uguaglianza delle derivate parziali seconde miste. Va invece considerato il tempo necessario per rendersi conto dell'analogia solo parziale con le funzioni di un'unica variabile. Nello sviluppo del calcolo, l'analogia svolge un ruolo euristico essenziale ma - come è capitato altre volte nella storia della matematica - può risultare di freno quando si tratta di individuare il momento in cui il parallelismo si interrompe e occorre prendere altre strade."  

Dalla descrizione appena riscontrata si evince dunque che il calcolo differenziale di funzioni di più variabili reali è solo apparentemente equivalente a quello di una singola variabile, poiché sussistono differenze profonde.
Bene, adesso andiamo a scoprire un'applicazione delle derivate parziali in fisica.
Sicuramente rientrano nelle celebri equazioni di Maxwell inerenti all'elettromagnetismo.
Noi andremo tuttavia ad analizzare un argomento più semplice nel quale esse rivestono un ruolo importante: la propagazione degli errori.
Come saprete, in fisica non esistono delle misure precise/perfette, in quanto, se proviamo a misurare una certa grandezza, effettueremo sempre, nonostante la nostra accortezza, dei piccoli errori.
Anzi, potremmo aver effettuato una misura (all'apparenza) estremamente precisa, ad esempio, della lunghezza di un tavolo in centrimetri, ma sussistono sempre ordini di grandezza (millimetri, micrometri, nanometri, picometri, ecc.) che non abbiamo considerato.
Risulta quindi impossibile effettuare una misura precisa al 100%.
Le nostre misure saranno pertanto costituite da 2 valori:

1) migliore stima della grandezza: xbest;
2) incertezza (o errore) assoluto: δx.

Ergo, possiamo scrivere una certa misura (magari la lunghezza di un tavolo) come:




Si definisce anche il cosiddetto errore relativo, pari al rapporto tra l'incertezza assoluta e la migliore stima:






Esso è, a differenza dell'errore assoluto e della migliore stima, un numero puro, che può essere espresso anche in percentuale.
Ma se abbiamo una certa grandezza (più complessa della lunghezza di un tavolo, poiché dipende, poniamo, dal prodotto di altre grandezze) e vogliamo calcolarne l'incertezza, come facciamo?
Prendiamo una grandezza generica q, dipendente, ad esempio, dal prodotto di altre 2 grandezze casuali e indipendenti (x e y).
In simboli abbiamo la funzione q = xy.
Le 2 grandezze avranno rispettivamente incertezze δx e δy.
Per trovare l'incertezza di q, cioè δq, dobbiamo sfruttare la formula generale della propagazione degli errori (basata sulle derivate parziali):






Per fare un esempio concreto, supponiamo che le grandezze x e y abbiamo le seguenti misure:

• x = 3,0 ± 0,1
• y = 2,0 ± 0,1

La migliore stima di q sarà: qbest = 6,0.
Ma qual è l'incertezza δq, se q = xy?
Calcoliamo in primis le derivate parziali (prime) della funzione q = xy.









Sicché otteniamo:





Sostituendo i valori forniti nell'espressione abbiamo che δq = 0,36.
La nostra misura di q avrà dunque valore 6 ± 0,36, o meglio, 6 ± 0,4.
Tirando le fila del discorso, abbiamo analizzato 2 importanti nozioni dell'analisi matematica (l'integrale definito e le derivate parziali), senza trascurare i particolari storici relativi ad esse, e ci siamo resi conto della loro importanza in fisica e, di conseguenza, nello studio della natura che ci circonda!