Ne parleremo qui in relazione alle sole matrici; infatti, tali argomenti potrebbero essere affrontati da un punto di vista più generale (e leggermente più complicato).
Ci accontenteremo, per il momento, della trattazione inerente alle nostre amate matrici.
Innanzitutto, per chi si fosse perso i post precedenti sulle matrici (prerequisiti per leggere senza problemi il presente articolo), ve li elenco immediatamente in ordine cronologico:
- "Metodo di Gauss-Jordan e sue origini antiche";
- "Matrici: il concetto di determinante";
- "Rango!!!";
- "Matrici inverse".
Incominciamo a definire gli autovalori e gli autovettori.
Se abbiamo una matrice quadrata A, allora un numero λ è detto autovalore se:
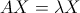.gif)
Ricordiamo che X rappresenta il vettore colonna delle incognite in un sistema di equazioni AX = b.
Possiamo facilmente notare che la condizione che definisce l'autovalore è immediatamente soddisfatta se X = 0.
Dunque, ai fini del rigore matematico, dobbiamo dire che quella definizione ha senso solo per qualche colonna X ≠ 0.
Tale colonna non nulla la chiamiamo appunto autovettore di A corrispondente all'autovalore λ.
Sussiste un problema: data una matrice quadrata A, come diavolo si possono trovare autovalori e autovettori?
Dobbiamo compiere delle manipolazioni sull'espressione:
.gif)
Nessuno ci vieta di scrivere questo:
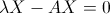.gif)
Ora raccogliendo la X (e tenendo presente che esiste la matrice identità I che ha la stessa funzione dell'1 nella moltiplicazione) abbiamo che:
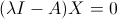.gif)
Quella appena scritta è l'espressione di un sistema lineare omogeneo, cioè un sistema di equazioni che ha come termini noti tutti 0 (in altre parole, la matrice dei termini noti b è una matrice nulla), tenendo però sempre presente che X deve essere diverso da 0.
Ecco un esempio di sistema omogeneo rappresentato in forma matriciale:
Una domanda importante: quand'è che effettivamente il sistema omogeneo non ricade nella soluzione X = 0, detta soluzione banale?
Un teorema dell'algebra lineare ci dice che questo accade se e solo se la matrice λI - A non risulta invertibile.
Ma qual è la condizione necessaria affinché una matrice A non sia invertibile?
Facile: il suo determinante deve essere pari a 0.
In simboli abbiamo:
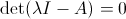.gif)
Da tale fatto scaturisce in maniera naturale un nuovo fondamentale concetto: il polinomio caratteristico.
Infatti, data una matrice quadrata A, il polinomio caratteristico di A risulta esprimibile attraverso la seguente formula:
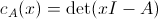
Visto? Niente di così astruso: al posto del numero λ abbiamo una variabile x, che è proprio la variabile del polinomio caratteristico.
Possiamo senza problemi asserire, basandoci su quanto scritto sopra, che λ è un autovalore della matrice A se e solo se:
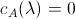.gif)
Detto in altri termini, λ è un autovalore di A se e solo se è una radice del polinomio caratteristico.
L'introduzione del polinomio caratteristico (e la sua strettissima relazione con l'autovalore) ci permette, inoltre, di trovare facilmente gli autovettori X.
Procediamo con un semplicissimo esempio!
Prendiamo la matrice:
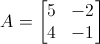.gif)
e troviamone il polinomio caratteristico, gli autovalori e gli autovettori.
Ricordiamo che il polinomio caratteristico è definito come:
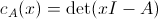
Cos'è xI?
Non è altro che il prodotto tra la matrice identità e l'incognita x.
Nel presente esempio abbiamo ovviamente una matrice identità di ordine 2.
Dunque:
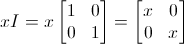.gif)
A questa matrice dobbiamo sottrarre la matrice A:
Per trovare il polinomio caratteristico, non ci resta che calcolare il determinante di tale matrice:
Scriviamo un po' meglio il polinomio caratteristico:
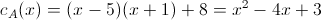.gif)
Il primo punto è fatto!
A proposito di "fatto":
OK, ritorniamo seri; il nostro prossimo compito sarà trovare gli autovalori.
Semplicissimo: basterà porre il nostro polinomio caratteristico uguale a 0, dato che gli autovalori sono le radici del polinomio caratteristico.
Procediamo:
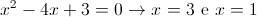.gif)
Ecco, λ₁ = 3 e λ₂ = 1 sono gli autovalori cercati!
Ah, ovviamente, nella risoluzione dell'equazione di 2° grado abbiamo adottato la nota formula (ridotta) per risolvere le equazioni del tipo ax² + bx +c = 0, con b multiplo di 2:
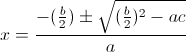.gif)
Adesso viene la parte leggermente più complicata: il rinvenimento degli autovettori.
Per trovare gli autovettori dobbiamo far riferimento all'espressione generale del sistema omogeneo:
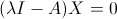.gif)
Ora basta sostituire a λ i valori degli autovalori individuati e rinvenire i rispettivi autovettori semplicemente risolvendo il sistema.
Incominciamo con:
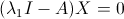.gif)
Sappiamo che:
Adesso ci basta risolvere il sistema rappresentato dalla matrice completa
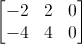.gif)
con l'ormai super noto metodo di Gauss-Jordan:
Alla fine della fiera rimaniamo con l'equazione:
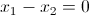.gif)
il che implica:
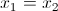.gif)
Ora poniamo
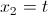.gif)
Possiamo pertanto concludere che la soluzione X (dunque gli autovettori) del nostro sistema è:
Ci sono infinite soluzioni al variare del parametro t e quindi infiniti autovettori relativi al singolo autovalore λ₁.
Per precisazione, questo insieme infinito di autovettori, relativi ad un singolo autovalore, viene chiamato autospazio.
Passiamo adesso a determinare gli autovettori inerenti a λ₂.
In tal caso abbiamo il sistema:
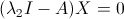.gif)
Troviamo che:
Ergo, la matrice completa associata al sistema omogeneo è:
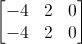.gif)
Utilizzando il metodo di Gauss-Jordan, immediatamente rimaniamo con un vettore riga:
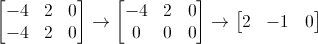.gif)
Ne deriva la seguente singola equazione:
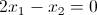.gif)
da cui:
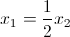.gif)
Ponendo come prima
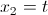
otteniamo infine che tutti gli autovettori X (ovvero l'autospazio) sono espressi dalla seguente relazione:
Una possibile "elegante" soluzione (tra le infinite) si ha quando t = 2; in tal caso, infatti, avremmo che:
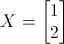.gif)
Nel caso non foste ancora convinti che quelli che abbiamo trovato siano effettivamente autovettori, possiamo persino effettuare un'ulteriore verifica.
Possiamo prendere come spunto la fondamentale uguaglianza:
.gif)
Praticamente, se X rappresenta un presunto autovettore, allora per essere certi che sia effettivamente un autovettore basta moltiplicarlo alla matrice A di partenza e osservare se il risultato è un multiplo di X stesso, ovvero X moltiplicato un numero λ (l'autovalore relativo a X).
Tuttavia, sorge un problema: come si moltiplica una matrice per un'altra matrice?
Innanzitutto, date 2 matrici generiche A e B, esse risultano moltiplicabili se e solo se il numero di colonne di A è uguale al numero di righe di B.
In caso contrario, non si possono moltiplicare!
Stabilita tale premessa, cerchiamo di spiegare nel modo più semplice possibile come si moltiplicano 2 matrici.Partiamo con il caso di 2 generiche matrici quadrate di ordine 2:
.gif) |
| matrice 2 × 2 |
.gif) |
| matrice 2 × 2 |
La matrice AB sarà:
.gif) |
| matrice 2 × 2 |
Come caspita abbiamo fatto?
Praticamente abbiamo costruito una matrice di questo genere:
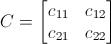.gif)
Ad esempio, c₁₁ è costruito prendendo la prima riga di A, la prima colonna di B e moltiplicandole fra loro.
Abbiamo dunque che:
L'elemento c₁₂, invece, sarà il prodotto tra la prima riga di A e la seconda colonna di B:
Completiamo il quadro!
Per quanto concerne c₂₁, dobbiamo prendere in considerazione (dato che il primo pedice, quello riferito ad A, è 2) ovviamente la seconda riga di A e la prima colonna di B (d'altronde il secondo pedice, quello riferito a B, è 1):
Finiamo con c₂₂, che sarà il prodotto tra la seconda riga di A e la seconda colonna di B:
Pertanto, abbiamo trovato le componenti di C e sappiamo che:
Non è poi così complicato moltiplicare le matrici!
Riassumendo, basta andare a moltiplicare ogni riga della 1° matrice con ogni colonna della 2° matrice e posizionare i vari risultati ottenuti nella giusta collocazione, cioè tenendo presente quale riga e quale colonna si sta prendendo in considerazione nel momento del calcolo.
Abbiamo osservato il caso particolare di 2 matrici quadrate.
Adesso eseguiamo la moltiplicazione tra 2 matrici non entrambe quadrate:
 |
| matrice 2 × 2 |
.gif) |
| matrice 2 × 1 |
Possiamo già dire, senza effettuare i calcoli, che la matrice AB risultante sarà una matrice 2 × 1, cioè un vettore colonna con 2 elementi.
Infatti, data una matrice generica T m × n e un'altra generica matrice S n × p, moltiplicabili in quanto il numero n di colonne di T è uguale al numero n di righe di S, allora il loro prodotto darà vita a una matrice m × p.
Semplice e bella questa osservazione, non vi pare?
Bene, ritornando al nostro prodotto AB, esso non è altro che:
.gif) |
| matrice 2 × 1 |
Non vi fornisco i vari passaggi poiché, ormai, dovrebbero essere chiari; se ancora non lo fossero, vi consiglio di guardare la seguente splendida immagine illustrativa del metodo di moltiplicazione tra matrici:
 | ||||
| prodotto tra matrice A 4 × 2 e matrice B 2 × 3 |
Dopo questa lunga (ma necessaria) peregrinazione tra matrici moltiplicate, ritorniamo alla nostra verifica sugli autovettori.
Ricordo che avevamo la matrice quadrata A
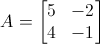.gif)
e avevamo trovato gli autovettori X relativi ai 2 autovalori λ₁ e λ₂.
Facciamo la prova con l'autovettore:
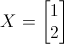.gif)
Abbiamo che:
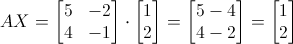.gif)
Come potete osservare, facendo la moltiplicazione otteniamo un multiplo dell'autovettore X (in realtà, in questo caso particolare, otteniamo l'autovettore stesso, o meglio, 1 moltiplicato l'autovettore).
Provate da soli a verificare che ciò accade anche per qualsiasi altro autovettore.
Ora passiamo ad illustrare finalmente la diagonalizzazione.
Ricordiamo che una matrice diagonale D è una matrice del tipo:
ove quei λ sono ovviamente numeri.
Ora, data una matrice quadrata A, diagonalizzare significa, in sostanza, determinare una matrice invertibile P tale che valga la seguente identità:
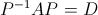.gif)
Ne consegue che una matrice quadrata A è detta diagonalizzabile se:
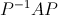.gif)
è una matrice diagonale per qualche matrice quadrata P invertibile.
Questa particolare matrice P viene denominata matrice diagonalizzante per A.
Inoltre, la matrice P si può anche scrivere nel seguente modo:
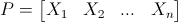.gif)
I termini X₁, X₂, ... , Xn non sono altro che le colonne di P.
C'è un importante teorema relativo alla diagonalizzazione: esso afferma che, data una matrice quadrata A:
1) A è diagonalizzabile se e solo se ha autovettori X₁, X₂, ... , Xn tali che la matrice
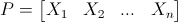
risulti invertibile;
2) Nel caso si verificasse il punto 1), allora varrebbe la relazione:
in cui, per ogni i, λi rappresenta l'autovalore di A associato a Xi.
Ecco, per diagonalizzare una matrice A non dobbiamo far altro che sfruttare il teorema appena citato.
Procediamo dunque con un illuminante esempio.
Proviamo a diagonalizzare la seguente matrice quadrata A di ordine 3:
Innanzitutto dobbiamo trovare il polinomio caratteristico, gli autovalori e gli autovettori.
Procediamo passo passo:
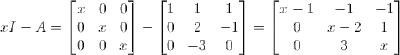
Quindi:
Per trovare il determinante, procediamo con lo sviluppo di Laplace sulla 1° colonna:
ovvero:
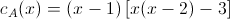
o meglio:
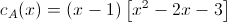
Ponendo
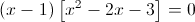.gif)
ne deriva che i nostri autovalori sono: λ₁ = 1, λ₂ = -1, λ₃ = 3.
Andiamo alla ricerca dei rispettivi autovettori!
Per quanto concerne λ₁ = 1 abbiamo:
Prendiamo la matrice completa associata al sistema omogeneo e applichiamo Gauss-Jordan:
ciò implica:
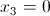.gif)
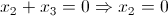.gif)
Inoltre, essendo x₁ indeterminato, abbiamo che:
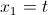.gif)
Dunque, il nostro autovettore relativo a λ₁ è:
Compiendo il medesimo procedimento per λ₂ e λ₃, otteniamo gli autovettori:
Ora, trovati finalmente gli autovettori e sapendo che:
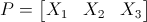.gif)
possiamo andare a sostituire appunto gli autovettori nell'espressione appena riportata, ottenendo:
L'ultimo passo da fare nel procedimento di diagonalizzazione è verificare se P risulta invertibile.
Vi dico, senza esplicitare ulteriori calcoli, che, in questo esempio, P è invertibile.
Provate voi, magari, a verificare che P sia effettivamente invertibile trovando il suo determinante (potreste sfruttare lo sviluppo di Laplace sulla 1° colonna) e constatando che risulta diverso da 0.
Come vi ho annunciato, P è invertibile; ciò implica che
Quella che osservate è la splendida matrice diagonale che deriva dal nostro procedimento di diagonalizzazione.
Vi starete forse chiedendo, dopo esservi sorbiti un vero e proprio festival delle matrici, a cosa possa mai servire concretamente la diagonalizzazione.
Per il momento, vi dico solamente che gli autovalori, gli autovettori e la diagonalizzazione rappresentano strumenti importantissimi nel campo della Meccanica Quantistica e della chimica quantistica.
La ragione sta nel fatto che l'equazione di Schrödinger indipendente dal tempo è un'equazione agli autovalori, sebbene, specifichiamo, nella maggior parte delle situazioni fisiche in uno spazio dimensionale infinito: lo spazio di Hilbert (di esso ne abbiamo parlato un pochettino nell'introduzione al Carnevale della Fisica n.30).
A seguito di tutta questa fatica, ci vuole assolutamente un po' di relax!
Ecco allora, a mo' di conclusione, 2 splendidi video musicali, concernenti rispettivamente la "Sonata Patetica" (2° movimento) di Beethoven e il 2° movimento del Concerto per Pianoforte n.21 (Elvira Madigan) di Mozart, interpretati in modo estremamente singolare:

.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)




















Ciao! :-D...molto chiaro e utile il tuo post, ma mi piacerebbe capire se si può diagonalizzare l'intero sistema Ax=b oltre alla sola matrice A, e se diagonalizzare può ridurre i calcoli nella risoluzione di sistemi in cui A è costante mentre b continua a cambiare. Grazie
RispondiEliminaCiao! :-D...molto bello e utile il tuo post, ma vorrei sapere una cosa. Immagina di risolvere sistemi lineari Ax=b, in cui A rimane costante mentre b continua a cambiare. Si può diagonalizzare l'intero sistema, e non solamente la matrice A, per ridurre il costo computazionale? grazie
RispondiEliminaInnanzitutto grazie dell'apprezzamento!
EliminaCome scritto nel post, la diagonalizzazione è un processo che si può applicare solamente a delle matrici quadrate. In un sistema del tipo Ax = b potremmo avere magari A matrice diagonalizzabile, ma b è un vettore colonna, ossia una matrice m righe x 1 colonna.
Sussistono magari dei casi in cui se consideri la matrice completa (ottenuta accostando alla matrice A il vettore colonna b) Ab essa risulta quadrata e diagonalizzabile, ma ciò ovviamente non accade sempre. Anzi, supponendo che A sia una matrice quadrata, considerando la matrice completa Ab, essa non sarà quadrata e quindi non diagonalizzabile!
Per completezza, esiste la diagonalizzazione simultanea di matrici diagonalizzabili (guarda qui), però le 2 matrici devono essere entrambe quadrate e soddisfare un altro specifico requisito illustrato nel file linkato.