La geometria che si studia a scuola è basata sul sistema assiomatico di Euclide, nella conformazione moderna fornitagli, al termine del XIX secolo, nell'opera Fondamenti della Geometria, da David Hilbert, il quale, per chi non lo sapesse, è colui che nel 1900, ad una conferenza tenutasi a Parigi, stabilì una lista di 23 importantissimi problemi matematici da risolvere (alcuni dei quali effettivamenti dipanati).
La geometria, come sappiamo, prende come riferimento alcuni enti primitivi (punto, retta, piano) e alcuni assiomi fondamentali su cui basare tutti i teoremi e le nozioni geometriche che conosciamo.
Bisogna riconoscere ad Euclide il merito di aver introdotto (in geometria) un sistema deduttivo e rigoroso, il quale consente a un teorema (matematico appartenente a qualsiasi branca) di essere valido per sempre, a condizione che venga dimostrato.
Questa è la base dello sviluppo matematico: considerare un certo enunciato (ipotesi, congettura, ecc.) e fornirne una dimostrazione che non lasci spazio a discussioni!
Tale procedimento è valido dalle questioni più "stupide", come accertarsi che 1 è maggiore di 0, fino alle questioni più complesse, spinose e importanti dell'intero universo matematico, come, ad esempio, la dimostrazione dell'ipotesi di Riemann concernente i numeri primi.
Risulta pertanto necessario affermare che la geometria euclidea, seppur antica di millenni, rimane sempre valida e riesce a spiegare in maniera molto accurata la realtà quotidiana che ci circonda.
Nella descrizione delle strutture del nostro Universo servono invece le cosiddette geometrie non euclidee, per la cui trattazione vi rimando all'articolo "Geometria euclidea: no, geometrie non euclidee!" .
Ora però spalanchiamo le porte ad un mondo più astratto, quello dell'algebra lineare, che sta alla base della moderna geometria analitica, sviluppatasi alla fine del XIX secolo.
La suddetta geometria si fonda sul concetto di vettore.
Il vettore, nel modo più semplice possibile, si può definire un segmento orientato avente 3 caratteristiche fondamentali:
1) modulo o intensità: equivale alla lunghezza del segmento, cioè al valore numerico che esprime;
2) direzione;
3) verso.

Se 2 vettori possiedono la stessa direzione, lunghezza e verso, si dicono equipollenti.
Se vogliamo essere più pignoli, "equipollenti" significa che tali segmenti orientati giacciono su rette parallele (eventualmente coincidenti) e si possono sovrapporre in modo che i loro punti iniziali e finali coincidano perfettamente.
Una delle motivazioni principali della scelta dei vettori come base su cui fondare la geometria risiedeva nella necessità di esprimere le leggi dell'elettromagnetismo in modo indipendente dalle coordinate.
Non a caso, fra i creatori della teoria c'è persino Maxwell, il padre dell'elettromagnetismo, assieme al fisico matematico Josiah Willard Gibbs e al fisico e ingegnere Oliver Heaviside, noto soprattutto per la funzione a gradino che prende il suo nome:

A detta dello storico della matematica Morris Kline, Heaviside riteneva l'analisi vettoriale "una forma abbreviata dell'ordinaria geometria analitica cartesiana".
Precisiamo che la scuola di pensiero fondata negli anni '40 dell'Ottocento da Gibbs e Heaviside, a differenza di quella sviluppata da William Hamilton (per maggiori informazioni vi rimando all'articolo "2 termini celebri in matematica: indeterminato e impossibile"), separava le componenti scalare (lo scalare è un numero puro) e vettoriale del quaternione (a + bi + cj + dk) e le considerava entità indipendenti fra loro.
Gibbs e Heaviside aprirono la strada alla moderna analisi vettoriale non per ragioni di pura matematica, bensì per ragioni relative alla fisica: cercavano infatti un'algebra che facesse al caso loro, e se questo voleva dire fare a pezzi i quaternioni di Hamilton, non si ponevano nessuno scrupolo.
Adesso, per proseguire nella trattazione, dobbiamo introdurre un concetto molto importante in geometria, ovvero quello di campo.Un campo è una terna (K, +, ∙) formata da:
- un insieme non vuoto K;
- 2 operazioni binarie su K, ossia 2 applicazioni:
2) ∙:K×K→K
denominate rispettivamente "somma" e "prodotto", che associano ad ogni coppia di elementi (a,b) appartenenti (∈) a K×K rispettivamente un elemento:
- a + b ∈ K ("somma di a più b");
- ab ("prodotto di a per b"),
in modo tale che risultino soddisfatti i seguenti assiomi:
K1) Commutatività della somma: a + b = b + a per ogni (∀) a,b ∈ K;
K2) Associatività della somma: a + (b + c) = (a + b) + c ∀a,b,c ∈ K;
K3) Esistenza dello zero: esiste (∃) un elemento 0∈K tale che (⎮) a + 0 = 0 + a = a ∀a ∈ K;
K4) Esistenza dell'opposto: ∀a ∈ K ∃a' ∈ K ⎮a + a' = 0;
K5) Commutatività del prodotto: ab = ba ∀a,b ∈ K;
K6) Associatività del prodotto: a(bc) = (ab)c ∀a,b,c ∈ K;
K7) Esistenza dell'unità: ∃1∈K ⎮a1 = 1a = a ∀a ∈ K;
K8) Esistenza dell'inverso: ∀a ∈ K, a ≠ 0, ∃a∗ ∈ K ⎮aa∗ = 1;
K9) Distributività della somma rispetto al prodotto: a(b + c) = ab + ac ∀a,b,c ∈ K;
K10) Non-esistenza di divisori dello zero: se ab = 0 e b ≠ 0, allora a = 0.
Se la terna (K, +, ∙) soddisfa gli assiomi K1,...,K7,K9,K10, ma non necessariamente K8, essa è detta: dominio (o dominio d'integrità).
Con le tradizionali operazioni l'insieme Z dei numeri interi relativi è un dominio.
Invece, gli insiemi Q (numeri razionali), R (numeri reali), C (numeri complessi), assieme alle loro operazioni sono campi.
Una piccola divagazione a proposito degli insiemi numerici fondamentali: alcuni matematici hanno ideato un modo simpatico e bizzarro per farli ricordare: basta tenere a mente la frase senza senso "Nine Zulu Queens Ruled China" (Nove regine zulù governavano la Cina) ed il gioco è fatto!
Infatti, ciascuna iniziale delle parole contenute nella frase sopracitata rappresenta un insieme numerico fondamentale: N,Z,Q,R,C!
Ora, ritornando seri, andiamo a vedere cos'è una matrice.
Una matrice A di tipo (m,n) (possiamo anche chiamarla matrice m × n) con m,n interi positivi, a elementi in un campo K è una tabella rettangolare di numeri
disposti in m righe e n colonne.
aij è il numero che si trova sulla i-esima riga e sulla j-esima colonna di A.
In termini più rigorosi si dice che aij è l'elemento di posto (i, j) della matrice A.
Di seguito alcuni semplici esempi di matrici:




In particolare, nel secondo caso abbiamo di fronte una matrice quadrata (presenta lo stesso numero di righe e colonne), nel terzo caso abbiamo una matrice unità (o matrice identità o matrice identica) e nel quarto caso una matrice nulla (o matrice zero).
Consideriamo ulteriori 2 esempi:


La prima matrice, costituita da 3 righe e da una sola colonna, è un esempio di vettore colonna, mentre la seconda matrice, formata da 3 colonne e una riga, rappresenta un caso di vettore riga.
Detto ciò, sorge una domanda, che cos'è il metodo di Gauss-Jordan a cui allude il titolo dell'articolo e cosa ha a che spartire con tutto ciò descritto in precedenza?
Il metodo (di eliminazione) di Gauss-Jordan non è altro che un importante metodo (dell'algebra lineare) di risoluzione dei sistemi di equazioni, il quale sfrutta pure le sopracitate matrici!
Consideriamo quindi un generico sistema di equazioni lineari:
Esso è un sistema di m equazioni lineari nelle n incognite X1,...,Xn.
Il sistema viene definito omogeneo se b1 = b2 = ... = bm = 0.
In caso contrario, il sistema è ovviamente detto non omogeneo.
Dal sistema possiamo ricavare una particolare matrice, denominata matrice dei coefficienti A:
Adesso raggruppiamo le incognite per formare il vettore x delle incognite:

e pure i termini noti per costituire il vettore b dei termini noti:

Si può inoltre definire la matrice completa (o orlata), ottenuta aggiungendo ad A il vettore colonna b:
Per indicare in maniera semplice il sistema possiamo pertanto utilizzare l'espressione Ax = b.
Ad esempio, prendendo il sistema:

Otteniamo la matrice completa:

Abbiamo dunque visto che qualunque sistema di equazioni lineari può essere trascritto in una matrice orlata (e viceversa).
Ma come si risolve un sistema?
Un procedimento di risoluzione è appunto l'algoritmo di Gauss-Jordan.
Il suddetto metodo consente infatti di stabilire se il sistema risulta compatibile (ovvero se ammette soluzioni) oppure no, e nel caso sussistano soluzioni, permette di trovarle tutte.
Il procedimento consiste nel sostituire il sistema dato con un sistema "triangolare" ad esso equivalente, ottenuto tramite una serie di passaggi chiamati "operazioni elementari sulle equazioni del sistema".
Tali operazioni corrispondono ad altrettante operazioni sulle righe della matrice completa.
Ergo, osserviamo quali sono le operazioni elementari che si possono attuare sulle equazioni di un sistema:
1) scambiare fra loro 2 equazioni del sistema;
2) moltiplicare (primo e secondo membro) di un'equazione per uno stesso scalare non nullo;
3) sostituire un'equazione con quella ottenuta sommando ad essa un multiplo di un'altra equazione.
Queste operazioni si possono tradurre, nell'ambito delle matrici, come operazioni sulle righe di una matrice:
1) scambiare tra loro 2 righe della matrice;
2) moltiplicare una riga della matrice per uno scalare non nullo;
3) sostituire una riga della matrice con quella ottenuta sommando ad essa un multiplo di un'altra riga.
Pertanto, trattasi di operazioni veramente semplici da comprendere e da attuare.
Ora mettiamo in pratica il metodo di Gauss-Jordan: riprendiamo il sistema precedente:

Dobbiamo ottenere, mediante le operazioni elementari elencate sopra, un sistema che permetta una "sostituzione all'indietro", cioè un sistema che nella prima equazione presenti tutte e 3 le incognite (x,y,z), nella seconda equazione 2 incognite (y,z) e nella terza un'incognita (z).
È sicuramente più facile capire il concetto risolvendo esplicitamente il sistema: procediamo!
Abbiamo il sistema; il nostro primo obiettivo è quello di eliminare x dalla seconda e terza equazione.
Come facciamo?
Semplice: utilizziamo le operazioni elementari.
Dunque, sottraiamo 2 volte la prima equazione dalla seconda e sottraiamo -1 volte la prima equazione dalla terza.
Otteniamo così il sistema equivalente:

Il coefficiente 2 della prima equazione si dice primo pivot.
Abbiamo eliminato la x dalla seconda e terza equazione: adesso dobbiamo eliminare la y dalla terza equazione.
A tal scopo sottraiamo -1 volte la seconda equazione dalla terza:

Il coefficiente -8 della seconda equazione è chiamato secondo pivot, mentre il coefficiente 1 della terza equazione è detto terzo pivot.
Finalmente siamo giunti ad un sistema equivalente (in una forma "triangolare) che ci permette di trovare le soluzioni sostituendo all'indietro.
Alla fine le soluzioni sono: z = 2, y = 1, x = 1.
Lo stesso però si può fare in maniera molto più rapida sfruttando le matrici.
Riprendiamo la matrice completa associata al sistema di partenza:

Il nostro obiettivo sarà rendere 0 il primo valore della seconda riga, e rendere 0 i primi 2 valori della terza riga, ovviamente attraverso le operazioni elementari sulle righe.
Non abbiamo fatto altro che lo stesso procedimento di prima, questa volta, tuttavia, con le matrici, ottenendo una matrice a gradini (o a scala).
Se volete la conferma che il risultato è lo stesso, riscrivete l'ultima matrice sotto forma di sistema e vedrete che è esattamente uguale a quello da cui abbiamo ricavato le soluzioni (z = 2, y = 1, x = 1) in precedenza.
Facciamo un ulteriore esempio, questa volta con un sistema avente 4 equazioni e 4 incognite:

Procediamo direttamente con il metodo di Gauss-Jordan per le matrici; ergo, scriviamo la matrice completa:

La prima cosa da fare è far diventare 0 il primo termine della seconda riga: addizioniamo la seconda riga con la prima riga moltiplicata per -1:

Ora, cerchiamo di far diventare 0 il primo elemento della terza riga, sommando -1 volte la prima riga alla terza riga:

Adesso possiamo fare una bella e assai conveniente cosa: scambiamo fra loro la seconda e la terza riga:

Ora dobbiamo solamente sistemare l'ultima riga: innanzitutto sommiamo -2 volte la prima riga alla quarta riga:

Dopodiché, sommiamo -1 volte la seconda riga alla quarta:

Infine, sommiamo 4 volte la terza riga alla quarta riga:

Finalmente abbiamo una matrice a gradini!
Scrivendo il sistema associato e risolvendo con sostituzione all'indietro otteniamo i risultati:- w = 3;
- z = -1;
- y = 2;
- x = 1
A proposito di tale metodo, Gauss scrisse che “grandemente riduce il tedio dei calcoli meccanici, successo avrà chi lo utilizza”.
Ma qual è esattamente la storia del metodo di Gauss-Jordan?
Forse non ci crederete, ma per risalire alle origini del suddetto metodo dobbiamo fare un pazzesco salto temporale all'indietro, verso l'antica Cina.
Gli antichi cinesi furono i primi ad utilizzare un sistema di numerazione posizionale, un migliaio di anni prima degli occidentali, per fare i calcoli con delle bacchette di legno.
Per i cinesi i numeri assunsero da sempre un ruolo di primo piano nella loro vita: si narra addirittura che fu l'Imperatore Giallo (Huang Di), intorno al 2400 a.C. circa, a chiedere alle divinità di creare la Matematica.
La Matematica era di importanza vitale per il buon funzionamento del regno, un regno gigantesco e in continua espansione.
L'Impero necessitava di abili amministratori, competenti appunto in Matematica.
Per istruire i funzionari veniva quindi utilizzato un manuale denominato "Nove capitoli sulle arti matematiche" (Jiuzhang Suanshu).
Da prove interne all'opera e da alcuni commenti apportati dai curatori delle ultime versioni, possiamo datare il libro originale dei Nove capitoli al tempo della dinastia degli Han "anteriori", la quale regnò dal 202 a.C. al 9 d.C.
Questo fu uno dei periodi di massimo splendore nella storia cinese, il primo nel quale l'Impero raggiunse un'estensione paragonabile alla Cina moderna.
Il testo, rappresentante il più autorevole trattato matematico antico cinese, è una raccolta di 246 problemi, inerenti questioni relative al commercio e al pagamento delle tasse.
Nel 263 d.C., il matematico Liu Hui scrisse e pubblicò un libro con le soluzioni ai problemi presenti nei Nove capitoli.
Si ritiene che proprio Lui Hui sia colui che ha ideato un metodo precursore del moderno algoritmo di Gauss-Jordan.
Infatti, nell'ottavo capitolo del noto testo antico cinese, è presente un problema sulla misura del grano.
L'enunciato del problema è questo:
"Ci sono 3 tipi di grano. 3 cesti del primo tipo, 2 del secondo e uno del terzo pesano complessivamente 39 misure. 2 cesti del primo, 3 del secondo e uno del terzo pesano 34 misure. E un cesto del primo, 2 del secondo e 3 del terzo pesano 26 misure. Quante misure di grano sono contenute in un cesto di ogni tipo?"
Possiamo riscrivere il problema in forma moderna, mediante un sistema di equazioni lineari:

Ovviamente, per quanto ci riguarda, la risoluzione del sistema non crea particolari difficoltà, ma come lo ha risolto Liu Hui?
Innanzitutto, moltiplica la seconda equazione per 3 (ottenendo così 6x + 9y + 3z = 102); poi sottrae la prima equazione da questa 2 volte.
In maniera analoga, moltiplica la terza equazione per 3 (ottenendo 3x + 6y + 3z = 78) e sottrae la prima equazione da questa una sola volta.
In tal modo, ottiene il sistema:

Egli moltiplica a questo punto la terza equazione per 5 (ottenendo 20y + 40z = 195) e sottrae dal risultato la seconda equazione 4 volte.
La terza equazione diviene allora: 36z = 99, ossia z = 11/4.
Sostituendo questo valore nella seconda equazione si ricava y = 17/4 e poi x = 37/4.
MA QUESTO NON È APPUNTO IL METODO DI GAUSS-JORDAN?
Esattamente: poniamo di nuovo in rilievo che un metodo di risoluzione di sistemi dell'algebra lineare, sviluppato nel XIX secolo, in realtà risale a quasi 2000 anni prima!Una sola parola: INCREDIBILE!
Dopo tali informazioni sbalorditive, ci proponiamo di far luce su altri 2 interrogativi finali:
1) in che occasione il celebre "princeps mathematicorum" Carl Friedrich Gauss introdusse il metodo?
2) chi è Jordan?
Gauss, fra il 1803 e il 1809, compì alcune osservazioni sull'asteroide Pallade e ne calcolò l'orbita.
Per riuscire nell'impresa, era necessario risolvere un sistema di 6 equazioni lineari in 6 incognite.
Mise dunque a punto il metodo di cui abbiamo parlato fino ad adesso.
E Jordan?
Wilhelm Jordan (1842-1899), nacque a Ellwangen, una piccola città nel sud della Germania.
Egli studiò all'instituto politecnico di Stoccarda.
Successivamente al lavoro, della durata di 2 anni, in veste di assistente ingegnere alle fasi preliminari della costruzione delle ferrovie, ritornò nel 1865 a Stoccarda come assistente in geodesia.
Dal 1881 fino alla sua morte fu professore di geodesia e geometria pratica all'università di Hannover.
Scrisse un manuale di geodesia (Handbuch der Vermessungskunde), rappresentante la sua opera più famosa.
L'algoritmo di Gauss-Jordan apparve nel 1888 nella terza edizione del suo manuale di geodesia.
Qual è il miglioramento apportato da Jordan al metodo tradizionale di Gauss?
Ebbene, Jordan ha fatto sì che il procedimento consenta di calcolare anche l'inversa di una matrice.
Aggiungo solo che una matrice quadrata A si dice invertibile se esiste una matrice M tale che AM = MA = I, dove I è la matrice identità.
Se esiste, M è unica ed è chiamata inversa di A, denotandola con la notazione A − 1.
Vorrei concludere con alcune considerazioni: siamo entrati nel mondo della geometria e abbiamo scoperto alcuni strumenti dell'algebra lineare.
Poi ci siamo soffermati sulle matrici e sul metodo di Gauss-Jordan.
La cosa che mi preme sottolineare nuovamente e maggiormente è però che tale procedimento, studiato oggi al liceo scientifico (forse) e in corsi universitari scientifici, risale a oltre 2000 anni fa.
Ciò è un piccolo ma significativo esempio del fatto che le civiltà antiche, a differenza di come comunemente ritenuto, erano veramente avanti in campo matematico e scientifico; dobbiamo a loro le fondamenta, le radici della nostra moderna cultura scientifica.





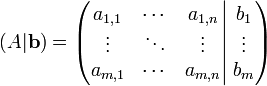










.gif)









Fantastico: ottimamente spiegato e piacevolissimo da leggere!
RispondiElimina