Probabilmente la base della matematica a livello elementare è rappresentata dalle equazioni.
Sin dalle scuole medie impariamo le basi per risolvere semplici equazioni, ossia uguaglianze tra termini numerici e letterali separate dal simbolo uguale (=).
Un esempio di equazione basilare è:
2x = 5
Il cui risultato è x = 5/2.
Le equazioni non sono sempre così semplici o così prive di altri elementi matematici fondamentali.
Sussistono equazioni di secondo grado, di terzo grado, di grado n, goniometriche, esponenziali, logaritmiche, con modulo, irrazionali, differenziali, alle derivate parziali, integrali e così via.
Esistono pure sistemi di equazioni, con n variabili ed m righe.
Immaginando un sistema di 2 equazioni di 1° grado, ossia di 2 rette, troveremo generalmente, risolvendo il sistema, il punto in cui le suddette rette si incontrano.
Ma come ben noto, non è sempre così.
Nei migliori casi, riscontreremo la soluzione e il sistema sarà determinato.
Se così non fosse, allora incorreremmo in soluzioni indeterminate o impossibili.
A cosa alludono tali termini?
Per illustrare questi concetti, è meglio proseguire mediante degli esempi chiari.
Prendiamo come esempio il sistema costituito dalle equazioni:
4x - 4y - 16 = 0
x - y - 4 = 0
Risolvendolo tramite uno dei metodi di risoluzione noti, come quello di sostituzione, di riduzione, ecc., riscontriamo la soluzione finale 0 = 0.
Il sistema risulta indeterminato, ossia ha un numero infinito di soluzioni.
Ciò, graficamente, sta a significare che le 2 rette rappresentanti le equazioni combaciano perfettamente.
Adesso, consideriamo quest'altro sistema:
5x = -3y - 9
100x + 60y = -80
Risolvendolo, troviamo la soluzione -100 = 0, il che non è mai vero.
Il sistema è appunto impossibile ed ergo: le 2 rette non si incontreranno in nessun punto.
Rimaniamo intorno al concetto di impossibile.
Consideriamo adesso l'equazione di 2° grado:
Sfruttando la formula (la cui forma attuale è stata pubblicata per la prima volta da Cartesio nel 1637 nell'opera La geometria) di risoluzione (ridotta) delle equazioni di 2° grado:
dove t = b/2, troviamo che

Cosa succede adesso?
L'equazione è stata risolta?
Ha fornito un risultato accettabile?
Assolutamente NO!
O meglio, almeno per quanto concerne il campo dei numeri reali.
Infatti, nell'insieme dei numeri reali R, l'equazione risulta impossibile, in quanto non esiste la radice quadrata di un numero negativo (nel caso in questione la radice di -6).
In realtà la questione può essere portata avanti e risolta, addentrandoci nel campo dei numeri complessi.
Rafael Bombelli (1530-1573) fu il primo, nel 1572, a riconoscere che anche le radici quadrate di numeri negativi posseggono una loro utilità.
Questi numeri vengono denominati oggi numeri immaginari, e assieme ai numeri reali vanno a costituire l'insieme dei numeri complessi.
Bombelli chiamava la √-1 più di meno, mentre il suo opposto, cioè -√-1 men di meno.
Inoltre, riconosceva che √-1 ⋅ √-1 = -1.
Traslato nel suo lessico: "Più di meno via più di meno fa meno".
Possiamo affermare allora che:


i è detta unità immaginaria.
Pertanto, i numeri complessi sono quei numeri che si possono scrivere come somma tra un numero reale e un numero immaginario:

dove x (chiamata parte reale) e y (detta parte immaginaria) sono numeri reali qualsiasi.
Ne consegue che i numeri reali non sono altro che numeri complessi aventi parte immaginaria pari a zero.
A proposito di numeri immaginari e complessi, come spiega Keith Devlin nel libro I problemi del millennio:
"Il numero i non è un numero reale; in altre parole non è un punto appartenente alla retta dei numeri reali. È tuttavia possibile moltiplicare i per un qualsiasi numero reale k per dare un nuovo numero ki. I numeri così ottenuti sono denominati "numeri immaginari". Per esempio, 5i è un numero immaginario. Nessuno dei numeri immaginari si trova sulla retta dei numeri reali (con la sola eccezione di 0i, che non è altri che lo zero). Dal punto di vista geometrico, i numeri immaginari formano una seconda retta, perpendicolare a quella dei numeri reali.

È possibile sommare un qualsiasi numero reale a un qualsiasi numero immaginario per ottenere un nuovo numero. Per esempio, possiamo sommare il numero reale 1 + 2/3 al numero immaginario 5i per ottenere il nuovo numero (1 + 2/3) + 5i. Queste combinazioni di un numero reale e di un numero immaginario sono denominate "numeri complessi". Dal punto di vista geometrico, i numeri complessi sono punti appartenenti al piano bidimensionale il cui asse x è la retta dei numeri reali e il cui asse y è la retta dei numeri immaginari. Il numero complesso (1 + 2/3) + 5i è il punto di ascissa (1 + 2/3) e di ordinata 5....I numeri complessi possono essere sommati, sottratti, moltiplicati e divisi, proprio come i numeri reali....Quando si eseguono operazioni su 2 numeri complessi, il risultato è un altro numero complesso. Pertanto, per fare dell'aritmetica, i numeri complessi sono proprio come i numeri reali, se non per il fatto che nel loro caso valgono regole un po' più complicate".
Sussistono inoltre importanti formule matematiche legate ai numeri complessi.
Ad esempio, c'è la formula di De Moivre, sviluppata dal matematico francese Abraham De Moivre (1667-1754).
La formula ci dice che per ogni numero intero maggiore o uguale a 1:
Tale formula, però, è un caso particolare di una formula più generale e ancor più importante, dovuta al grande matematico Eulero, la quale consente di definire l'operazione esponenziale per numeri complessi.
L'identità di Eulero afferma che l'esponenziale di un numero immaginario puro (per ogni ϑ ∈ R) può essere definito come:
Una conseguenza della suddetta espressione è la famosissima formula:
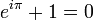
Tale equazione possiede una bellezza ed un'eleganza matematica insuperabile, in quanto riesce a mettere in relazione in una formula veramente sintetica (più sintetica di una poesia ermetica!) le 5 costanti più importanti della matematica (e, i, π, 1, 0), assieme agli operatori "somma", "moltiplicazione", "elevamento a potenza", "uguaglianza", altrettanto fondamentali in matematica.
L'equazione aveva colpito così profondamente i matematici tanto che Benjamin Pierce, durante una conferenza del 1864, esclamò: "Signori, non abbiamo la minima idea di che cosa significhi questa equazione, ma siamo sicuri che è qualcosa di molto importante". Riagganciandoci alla descrizione compiuta da Keith Devlin, dobbiamo specificare che il piano bidimensionale in cui vengono rappresentati i numeri complessi si chiama piano di Argand-Gauss e prende il nome ovviamente da Jean-Robert Argand (1768-1822) e Carl Friedrich Gauss (1777-1855).
Inoltre, ogni numero complesso possiede un "compagno", o in termini più rigorosi, un "coniugato".
Il coniugato di 1 + 2i è 1 - 2i, il numero che si ottiene cambiando di segno il secondo termine.
Dunque, allo stesso modo, il coniugato di 1 - 2i è 1 + 2i.
La cosa interessante è che sommando o moltiplicando 2 numeri coniugati si ottiene un numero reale.
Abbiamo quindi discusso riguardo ad alcune peculiarità dei numeri complessi.
Tuttavia, essi furono considerati in un certo qual senso "mistici", fin quando non furono oggetto di intenso studio da parte di Sir William Rowan Hamilton, il più eminente matematico irlandese del XIX secolo.
Riporto la splendida descrizione, intrisa di interessanti aneddoti, sulle scoperte di Hamilton inerenti i numeri complessi di John C. Baez e John Huerta, presente nel numero 515 della rivista Le scienze:
"Nel 1835, all'età di 30 anni, il matematico e fisico William Rowan Hamilton scoprì che è possibile considerare i numeri complessi come coppie di numeri reali. All'epoca i matematici scrivevano solitamente i numeri complessi nella forma a + ib ideata da Argand, ma Hamilton osservò che siamo liberissimi di pensare al numero a + ib come a un modo peculiare di scrivere 2 numeri reali: per esempio, (a,b). Questa notazione rende molto facile sommare e sottrarre i numeri complessi: basta sommare (o sottrarre) ogni numero della seconda coppia al corrispondente della prima coppia....Dopo che Hamilton ebbe inventato questo sistema algebrico per i numeri complessi, che avevano un significato geometrico, cercò per molti anni di inventare un'algebra più grande, fatta di terne di numeri che svolgessero un ruolo simile per la geometria tridimensionale: questi tentativi gli diedero frustazioni senza fine. Una volta scrisse al figlio: "Ogni mattina...quando scendevo per la colazione, il tuo (allora) fratellino William Edwin e tu mi chiedevate: "Allora, papà, sei riuscito a moltiplicare le terne?" Al che ero sempre obbligato a rispondere: "No, le so solo sommare e sottrarre". Anche se all'epoca non poteva saperlo, il compito che si era proposto era matematicamente IMPOSSIBILE. Hamilton cercava un sistema numerico tridimensionale in cui fosse possibile sommare, sottrarre, moltiplicare e dividere. La parte difficile è la divisione: un sistema numerico in cui è possibile dividere è detto ALGEBRA DI DIVISIONE. Solo nel 1958 3 matematici dimostrarono un fatto sbalorditivo che si sospettava da decenni: qualsiasi algebra di divisione deve avere dimensione 1 (il che vale solo per i numeri reali), 2 (numeri complessi), 4 o 8. Hamilton doveva cambiare le regole del gioco. Hamilton stesso arrivò a una soluzione il 16 ottobre 1843. Stava camminando con la moglie lungo il Royal Canal per andare a una riunione della Royal Irish Academy a Dublino, quando ebbe una rivelazione improvvisa. Le rotazioni in 3 dimensioni non si possono descrivere con 3 soli numeri. Aveva bisogno di un quarto numero, generando così un insieme quadrimensionale detto dei QUATERNIONI, che hanno la forma a + ib + jc + kd. Qui i numeri i, j e k sono 3 distinte radici quadrate di -1. In seguito Hamilton avrebbe scritto: "In quel momento sentii chiudersi il circuito galvanico del pensiero; e le scintille che ne sprizzarono erano le equazioni fondamentali che collegano i, j e k; esattamente nella forma in cui le ho sempre usate da allora". E, con un famoso atto di vandalismo matematico, incise queste equazioni nella pietra del ponte Brougham. Ora sono sepolte dai graffiti, ma c'è una lapide che ricorda la scoperta. Può sembrare strano che servano punti di uno spazio quadrimensionale per descrivere trasformazioni di uno spazio tridimensionale, ma è proprio così...Hamilton passò il resto della vita nell'ossessione per i quaternioni, e ne scoprì molti usi pratici. Oggi in molte di queste applicazioni i quaternioni sono stati sostituiti dai loro cugini più semplici, i vettori, che si possono considerare come quaternioni dalla forma speciale ia + jb + kc (il primo numero è semplicemente zero). Eppure i quaternioni forniscono un modo efficiente per rappresentare le rotazioni tridimensionali in un computer e in questo contesto compaiono di continuo, dal sistema di controllo dell'assetto di un veicolo spaziale al motore grafico di un videogioco."
Altre informazioni interessanti su Hamilton le troviamo in Storia della matematica di Carl B. Boyer:
"Il padre di Hamilton, che esercitava la professione di avvocato, e sua madre, che era considerata una donna ricca di doti intellettuali, morirono entrambi quando il figlio era ancora bambino. Ma prima ancora che diventasse orfano, dell'educazione del giovane Hamilton si era preso curo uno zio che era studioso di lingue. Di ingegno eccezionalmente precoce, il giovane William all'età di 5 anni era già in grado di leggere il greco, l'ebraico e il latino; a 10 anni conosceva una mezza dozzina di lingue orientali. L'incontro, pochi anni più tardi, con un calcolatore prodigio fu forse la scintilla che accese il già forte interesse di Hamilton per la matematica...Hamilton fece i suoi studi universitari al Trinity College di Dublino, dove, ancora studente, all'età di 22 anni fu nominato Astronomo reale d'Irlanda, Direttore dell'Osservatorio dio Dunsink e Professore di astronomia. In quello stesso anno presentò all'Accademia irlandese una memoria sui sistemi di raggi, nella quale illustrò una delle sue idee predilette, ossia l'idea che lo spazio e il tempo sono "indissolubilmente connessi l'uno con l'altro". In un certo senso è possibile intravedere in questa teoria un'anticipazione della teoria della relatività...Durante gli ultimi 20 anni della sua vita Hamilton dedicò tutte le sue energie alla sua algebra prediletta, alla quale egli tentava di attribuire un significato cosmico e che alcuni matematici inglesi consideravano come una sorta di arithmetica universalis di tipo leibniziano. Le sue Lectures on Quaternions (Lezione sui quaternioni) furono pubblicate nel 1853, e negli anni successivi egli si dedicò alla preparazione di un ampio trattato intitolato Elements of Quaternions (Elementi di teoria dei quaternioni). Morì però nel 1865 prima di riuscire a condurne a termine la stesura: l'opera incompiuta fu pubblicata l'anno successivo a cura del figlio."
Tirando le fila del discorso, abbiamo intrapreso un viaggio all'interno delle equazioni matematiche che ci ha condotto sulla tematica dell'indeterminato e soprattutto dell'impossibile.
In particolare, quest'ultimo, come abbiamo potuto constatare, è stato inizialmente una sorta di "blocco" per i matematici, che non potevano risolvere alcune equazioni poiché restituivano risultati inaccettabili, come radice di -6.
Tuttavia, se andiamo a guardare la storia dell'impossibile in matematica sotto una differente prospettiva, riscontriamo che esso è stato la fonte di nuovi importantissimi sviluppi in tal ambito.
Prendiamo come esempio i pitagorici: quando essi hanno scoperto che alcune operazioni restituivano dei numeri irrazionali, come la radice di 2, sono rimasti sconvolti.
Anzi, desideravano occultare l'esistenza dei numeri irrazionali.
Poi, però, questi numeri sono stati accettati e oggi fanno parte del più completo insieme dei numeri reali.
Andando avanti, i numeri reali, in certe equazioni, ad esempio di 2° grado, portano a risultati impossibili, come radice di -2.
Tale blocco ha fatto sì che i matematici sviluppassero i numeri immaginari e i numeri complessi, in cui tale risultato non è più inaccettabile ma fa parte dell'ordinario.
Anzi, i numeri reali sono solamente casi particolari dei numeri complessi.
Dopodiché, Hamilton voleva estendere l'algebra ai numeri tridimensionali, ma non riusciva nell'operazione di divisione.
Alla fine, capì che solo in 4 dimensioni ci può essere un algebra di divisione e si era arrivati alla scoperta dei quaternioni.
I vettori, studiati comunemente in matematica e fisica, in realtà non sono che delle semplificazioni dei quaternioni.
Dai quaternioni si arrivò agli ottetti, numeri in 8 dimensioni e dagli ottetti scaturirono fuori i sedenioni, in 16 dimensioni.
Tuttavia, questi ultimi, non costituiscono un'algebra di divisione, considerato che alcuni di essi sono addirittura divisori dello zero!
Pertanto, un'algebra "completa" si può costruire solo su numeri che hanno dimensione 1,2,4 o 8!
In conclusione, riporto 2 video musicali, il primo (il violinista David Garrett in Mission Impossible) inerente il tema dell'impossibile, il secondo (la violinista Sarah Chang nel presto dell'Estate dalle 4 Stagioni di Vivaldi) concernente invece il numero 4, visto che abbiamo parlato di quaternioni.
Buon Ascolto!









.gif)










Nessun commento:
Posta un commento