Infatti, se in un piano il cerchio è più simmetrico di un quadrato in quanto identico comunque lo si giri, nello spazio tridimensionale la sfera risulta più simmetrica del cerchio.
Basterà notare lo "spessore" del cerchio e rendersi conto che tutto ciò che lo rendeva straordinario nel piano non sussiste più nello spazio.
Per fare un esempio banale, un hula hoop non apparirà identico se osservato da posizioni differenti!
La sfera, invece, è sempre uguale da qualunque punto di vista la si guardi.
La sfera è dunque una figura geometrica di grande rilevanza: è stata persino alla base di imponenti modelli cosmologici.
Per non fare il solito esempio del sistema tolemaico-geocentrico, ve ne cito un altro, decisamente meno conosciuto: quello delle sfere omocentriche di Eudosso.
Eudosso di Cnido (409 a.C.-356 a.C.), eminente matematico, famoso soprattutto per il metodo di esaustione (di cui abbiamo parlato un po' qui), fu un discepolo di Platone.
A seguito dell'importante periodo formativo assieme al celebre filosofo, Eudosso si recò a studiare in Egitto, ove divenne allievo di un sacerdote di Eliopoli, il quale gli mostrò i risultati delle osservazioni planetarie eseguite dagli Egizi nel corso di decenni.
Tuttavia, nonostante le incessanti osservazioni e gli accurati studi, gli Egizi non fornirono alcuna spiegazione in merito al fenomeno delle retrogradazioni (cioè il movimento di alcuni pianeti in senso opposto rispetto a quanto ci si aspetterebbe).
Eudosso cercò di supplire a tale mancanza ipotizzando che ogni pianeta fosse in una sfera cristallina, perfettamente trasparente, concentrica con la Terra (da ciò deriva l'appellativo "omocentriche" fornito a queste particolari sfere).
A detta di Eudosso, la Terra risulta situata, totalmente immobile, al centro dell'Universo.
Attorno ad essa ruotano, a gruppi di 4, le sfere che portano, per ciascun gruppo, un pianeta.
La sfera più esterna del gruppo risulta inoltre incernierata su un perno che ruota a una velocità costante, dunque con un moto circolare uniforme.
Alla sfera più esterna è inoltre incernierata, su un altro perno inclinato rispetto al primo, una seconda sfera, anch'esso ruotante con moto uniforme, ma con una velocità differente da quella più esterna.
E poi ci sono le 2 sfere maggiormente interne, introdotte da Eudosso proprio per spiegare la retrogradazione.
La composizione dei moti delle 4 sfere ne fornisce uno che designa con buona approssimazione il moto apparente del pianeta, con le sue variazioni di velocità e retrogradazioni.
Certamente non era un'impresa da poco fissare accuratamente il diametro delle varie sfere, il loro asse di rotazione e le relative angolazioni e velocità, tuttavia il modello era comunque abbastanza buono per quanto concerneva i 5 pianeti allora conosciuti (Saturno, Giove, Marte, Venere, Mercurio).
Per il Sole e la Luna erano invece sufficienti 3 sfere per ciascuno e per le "stelle fisse" bastava una singola sfera.
Ergo, in complessivo, Eudosso aveva previsto un modello cosmologico costituito da: 5 × 4 + 2 × 3 + 1 = 20 + 6 + 1 = 27 sfere.
Vi consiglio vivamente di cliccare qui per visionare uno splendido video del Museo Galileo di Firenze inerente proprio alle sfere omocentriche.
Abbiamo brevemente introdotto l'argomento sfere; tuttavia, da adesso in poi, non parleremo più di sfere tradizionali, bensì di particolari sfere: la pseudosfera e la sfera cornuta di Alexander.
Esse sono decisamente diverse dalle sfere a cui si è abituati.
Cominciamo dalla pseudosfera!
Prima di dare il via alla trattazione, consiglio i lettori meno esperti di fare un salto all'articolo "Geometria euclidea: No, geometrie non euclidee!", poiché con le pseudosfere saremo appunto immersi nel mondo "non euclideo".
Si parte!
Immaginiamo di prendere una corda oppure una catenina che abbia la medesima densità in tutti i suoi punti e supponiamo anche di tenerla appesa afferrandola agli estremi.
Che figura geometrica si forma?
Sembrerebbe una parabola, ma, in realtà, è tutt'altra cosa!
La figura descritta si chiama (ma guarda un po' il caso) catenaria e l'equazione che la rappresenta è:
.gif)
Essa dipende dal parametro a: infatti la configurazione più semplice è:
.gif)
Ecco l'immagine illustrante come cambia la raffigurazione della catenaria al variare del parametro a:
Ora una questione lasciata in sospeso: cosa diavolo indica cosh x?
Certamente sapete che è un coseno, ma quello che vedete davanti è un coseno particolare: si chiama coseno iperbolico.
Soffermiamoci un po' sull'argomento.
Praticamente, le funzioni iperboliche rappresentano una famiglia di funzioni non trigonometriche ma che presentano effettivamente alcune proprietà analoghe alle tradizionali funzioni trigonometriche.
Esse vengono fuori da particolari combinazioni di funzioni esponenziali.
Osserviamo innanzitutto com'è definito il seno iperbolico:
.gif)
Ed ecco invece la definizione del coseno iperbolico:
.gif)
Così come nella trigonometria sussiste la relazione fondamentale:
.gif)
Allo stesso modo, per quanto concerne le funzioni iperboliche, è valida la relazione:
.gif)
Non ci credete? Volete la prova?
Allora andiamo a sostituire le definizioni di seno e coseno iperbolico all'interno della formula appena scritta:
Per il seno e il coseno iperbolico valgono persino le famose formule di addizione e sottrazione:
Ovviamente, conoscendo le definizioni di seno e coseno iperbolico, possono essere definite ulteriori funzioni, come la tangente e la cotangente iperbolica:
Ritorniamo ora alla nostra funzione catenaria.
Lo sapete che da essa possiamo ricavare un'altra curva molto particolare?
Osservate questa magnifica animazione:
La curva che viene disegnata in alto è ovviamente la catenaria, ma, allo stesso tempo, si delinea un'altra singolare curva (rappresentata in rosso): la trattrice.
La trattrice (dal latino tractrix, derivante a sua volta dal verbo trahere, cioè trainare), chiamata anche curva di inseguimento o curva di caccia, fu introdotta per la prima volta da Claude Perrault (fratello di Charles Perrault, autore di numerose e celebri fiabe, come Cenerentola, Cappuccetto rosso, ecc.) nel 1670 e studiata in seguito da Newton e da Christiaan Huygens.
Un'ulteriore singolare denominazione della trattrice è quella che deriva dal suo nome tedesco, Hundkurve, che significa "curva del cane (al guinzaglio)".
Praticamente, essa viene generata da un oggetto (oppure un punto) che risulta trascinato lungo un piano orizzontale (xy) da un certo "segmento trascinatore" di lunghezza costante.
Ciò implica che anche una circonferenza può dar luogo a una trattrice.
Immaginiamo una circonferenza centrata nell'origine degli assi cartesiani e di raggio 2.
La circonferenza, ovviamente, presenta un raggio costante, dunque un segmento che risponde ai requisiti richiesti per il segmento trascinatore.
Ecco a voi un applet, che ho realizzato con GeoGebra (cliccate qui), illustrante la suddetta situazione: Ma quali sono le equazioni rappresentanti la trattrice?
Se consideriamo, per semplicità, come catenaria quella data dall'equazione:
.gif)
dunque quella in cui il parametro a = 1, allora le equazioni parametriche designanti la trattrice sono le seguenti:


ove t è un parametro appartenente all'intervallo [0, 2π].
Ovviamente, non è detto che la trattrice debba svilupparsi orizzontalmente; può infatti svilupparsi anche rispetto all'asse y:
Dopo tutte queste elucubrazioni, vi starete probabilmente chiedendo: cosa c'entra tutto ciò con la pseudosfera?
Ebbene, la pseudosfera non è altro che la superficie ottenuta ruotando la trattrice!
Essa ricorda 2 trombe incollate fra loro lungo i bordi delle campane (ovvero delle parti finali delle trombe).
I bocchini delle trombe (cioè le parti degli strumenti che vanno a contatto con la bocca) sono dunque collocati alle 2 estremità, che tuttavia si estendono all'infinito.
 |
| Pseudosfera |
Un primo passo verso la scoperta di tale particolare superficie fu compiuto da Huygens.
Costui dimostrò che: "il volume (e la superficie) del solido generato dalla rotazione della trattrice intorno al suo asintoto è pari a metà del volume (all'area della superficie) della sfera di raggio uguale alla lunghezza costante della tangente".
Prima di proseguire la narrazione inerente alla pseudosfera, soffermiamoci un attimo su un concetto importante che non avevamo mai incontrato prima in questi lidi: l'asintoto.
In parole semplici, l'asintoto è una retta (orizzontale, verticale o obliqua) a cui una data curva si avvicina sempre più, senza mai toccarla.
Come potete notare, l'iperbole equilatera appena riportata non toccherà mai e poi mai gli assi cartesiani (che, in tal caso, rappresentano appunto gli asintoti)!
Entriamo un po' più nel dettaglio.
ASINTOTI VERTICALI
Data una certa funzione f(x), se il limite di questa funzione per x tendente a una quantità finita c risulta infinito, allora la retta x = c designa un asintoto verticale.
In termini più rigorosi:

Ovviamente, se avessimo voluto essere maggiormente precisi, avremmo dovuto scrivere 2 limiti, ossia quello destro e quello sinistro (di essi abbiamo parlato qui).
ASINTOTI ORIZZONTALI
Data una certa funzione f(x), se il limite di tale funzione per x tendente a un valore infinito risulta finito, cioè pari a un valore l, allora la retta y = l rappresenta un asintoto orizzontale.
In simboli:

ASINTOTI OBLIQUI
Gli asintoti obliqui sono leggermente più particolari.
Innanzitutto dobbiamo dire che una funzione presenta asintoti obliqui se e solo se non ha un asintoto orizzontale.
Ne deriva che certamente deve valere il seguente limite:

Entriamo nello specifico!
Una funzione f(x) ha come asintoto obliquo la retta y = mx + q se e solo se:

Ma come sono definiti i coefficienti m e q?
Nel seguente modo:


Ecco un esempio di asintoto obliquo:
Bene, abbiamo definito le 3 tipologie esistenti di asintoto (rappresentato da una retta).
Un monito: non è detto che una retta sia un asintoto per tutta l'estensione della funzione; potrebbe invece essere un asintoto soltanto in uno specifico intervallo.
Ecco un illuminante esempio:
Come vedete, la curva rappresentata nell'immagine interseca la retta y = 3 in un punto, ma, successivamente, per valori di x tendenti all'infinito, essa diviene un vero e proprio asintoto.
Compiamo un semplicissimo esempio di rinvenimento degli asintoti.
Prendiamo la funzione:

Come potete constatare, è una funzione razionale fratta.
Ne consegue che il denominatore deve essere diverso da 0.
Pertanto, vale la condizione:

Quindi sussiste un preciso campo di esistenza della funzione:

Ricordo che la parentesi tonda indica un intervallo aperto.
Per ricercare gli asintoti, non bisogna far altro che calcolare i limiti nei cosiddetti punti di accumulazione esterni al dominio della funzione e all'infinito.
Nel nostro caso, dobbiamo pertanto calcolare i limiti per x tendente ai valori 1 e infinito:
Questo risultato implica che la retta x = 1 è un asintoto verticale.
Procediamo con l'altro limite:
Ciò significa che la retta y = 2 è un asintoto orizzontale.
Ecco l'immagine raffigurante tutto ciò (gli asintoti sono le linee tratteggiate in rosso):

Bene, dopo questo piccolo excursus di analisi matematica, ritorniamo alla geometria e soprattutto alla pseudosfera.
Ci eravamo fermati alla scoperta effettuata dall'olandese Christiaan Huygens.
Dopo gli studi del fisico olandese, ulteriori ricerche sull'argomento vennero condotte dal matematico Ferdinand Minding (1806-1885).
Nato a Kalisz (città assai singolare, dato che tra il 1800 e il 1840 si ritrova ad essere prussiana, polacca e infine russa), Minding compì studi di fisica, filosofia e filologia all'Università di Halle e di Berlino, mentre per quanto concerne la matematica, fu totalmente autodidatta.
Egli pervenne alle sue più grandi scoperte nell'ambito della geometria differenziale delle superfici.
Nel 1839 Minding pubblicò un articolo sul Journal für die reine und angewandte Mathematik, in cui dimostrò che, se 2 superfici hanno curvatura costante e uguale, allora risultano localmente isometriche.
In termini un po' più semplici, è possibile applicare ogni porzione abbastanza piccola dell'una su una corrispondente porzione dell'altra senza innescare alterazioni nella misura delle lunghezze e degli angoli.
Ma cosa si intende per curvatura?
Il concetto di curvatura di una curva piana in un punto è stato definito da Newton nel 1671 e approfondito da Huygens nel 1673.
Per definirla rigorosamente, innanzitutto si considera il cerchio passante per il punto dato e per altri 2 punti della curva considerata, uno per lato.
Si fanno poi avvicinare i 2 punti laterali a quello dato, ottenendo al limite un cerchio detto osculatore, che approssima la curva in quel punto:
 |
| Curva e suo cerchio osculatore, tangente nel punto P |
Si può allora definire la curvatura K nel punto P come:

ossia come l'inverso del raggio del cerchio osculatore, detto raggio di curvatura.
Il segno della curvatura è positivo se il cerchio osculatore risulta situato al di sopra della tangente al punto stabilito, negativo in caso contrario.
Questa definizione di curvatura ha una sua concretezza giacché, se consideriamo ad esempio una strada, siamo soliti affermare che essa "curva molto" se fa una curva stretta, ovvero una curva con un raggio piccolo.
Dopodiché si passa a definire la curvatura di una superficie in un punto.
Nel 1767 il grande Eulero riuscì a ridurre il problema alla curvatura delle curve.
Il ragionamento adottato da Eulero è più o meno il seguente.
Si considera anzitutto il piano tangente alla superficie nel punto stabilito.
Subito dopo si considera la sezione di curva della superficie individuata da ciascun piano perpendicolare a quello tangente e passante per il punto dato.
Il prossimo passo consiste nel constatare che esistono una curvatura massima e una minima di tutte queste sezioni curve, e viene chiamata curvatura della superficie nel punto nient'altro che il loro prodotto.
Inoltre, la curvatura della superficie è positiva se le 2 curvature massima e minima presentano il medesimo segno; la curvatura negativa si ha ovviamente quando le 2 curvature massima e minima presentano, al contrario, segni opposti.
Nel contesto che stiamo analizzando, ci stiamo riferendo a superfici a curvatura costante, cioè che presentano la medesima curvatura dappertutto.
Nel piano euclideo le uniche curve a curvatura costante sono:
- la retta: ha curvatura nulla;
- il cerchio: ha curvatura positiva, pari all'inverso del suo raggio.
Nello spazio euclideo abbiamo diverse superfici a curvatura costante, fra cui:
- il piano: possiede curvatura nulla, poiché tutte le sue sezioni perpendicolari sono rette;
- la sfera: la sua curvatura è pari all'inverso del quadrato del raggio (1/r²), in quanto tutte le sue sezioni ortogonali sono dei cerchi massimi, ognuno dei quali ha curvatura pari a 1/r.
Detto ciò, facciamo ritorno alle ricerche di Minding.
Oltre quanto esplicato in precedenza, nel lavoro del 1839 Minding mostra alcuni esempi espliciti di superfici con curvatura costante negativa, tra cui la superficie di rivoluzione della trattrice (senza però indicarne una specifica denominazione).
L'anno seguente, sempre sulla rivista intitolata Journal für die reine und angewandte Mathematik, Minding illustra una significativa relazione: scambiando le funzioni iperboliche con quelle trigonometriche, le formule per la risoluzione dei triangoli geodetici su una superficie di curvatura costante negativa -1/k² si trasformano, come per magia, nelle formule per la risoluzione dei triangoli geodetici su una sfera di raggio R.La cosa buffa è che nonostante Minding pubblicò la sua ricerca nella stessa rivista su cui Lobaĉevskiĭ 3 anni prima aveva pubblicato alcuni suoi studi concernenti la geometria iperbolica, nessuno si accorse degli stretti legami sussistenti fra la pseudosfera e la suddetta geometria non euclidea.
Nessuno fino all'arrivo di Beltrami.
Eugenio Beltrami (1835-1900) nacque il 16 novembre 1835 a Cremona, la città del famoso liutaio Antonio Stradivari (1644-1737).
Espulso dal Collegio Ghislieri di Pavia per aver fomentato disordini contro il rettore e costretto quindi all'abbandono degli studi universitari a causa della mancanza di mezzi della famiglia, Beltrami accettò un "umile impiego amministrativo" senza mai conseguire una laurea.
Nonostante ciò, grazie all'appoggio diretto del "maestro" Francesco Brioschi (che all'epoca ricopriva il ruolo di segretario del Ministero della pubblica istruzione) e di Luigi Cremona, fu nominato, nel 1862, professore straordinario di Algebra complementare e di Geometria analitica all'Università di Bologna (trattasi di un favoritismo meritato, ma pur sempre un favoritismo!).
2 anni più tardi si trasferì, come professore ordinario, sulla cattedra di Geodesia dell'Università di Pisa, rimasta vacante a seguito della morte di Ottaviano Fabrizio Mossotti (1791-1863).
Beltrami, pensate un po', fu la seconda scelta di Enrico Betti, famoso matematico e personaggio di spicco all'interno della suddetta Università, il quale provò in primo luogo ad assegnare la cattedra nientedimeno che a Bernhard Riemann, che declinò l'allettante offerta a causa dell'insalubrità del clima pisano!
Beltrami, che aveva già effettuato diverse pubblicazioni relative alla geometria differenziale, dal momento in cui venne insignito del prestigioso incarico accademico, cercò di approfondire lo studio della cartografia, tanto da pubblicare, nel 1865, sugli Annali di matematica pura e applicata, un importante articolo dove dimostrò che le sole superfici che possono essere "riportate" su un piano in maniera tale che le geodetiche (curve che descrivono la traiettoria più breve tra punti di un particolare spazio, così chiamate da Joseph Liouville nel 1850) vengano rappresentate da linee rette sono quelle a curvatura costante.
Nel 1868 venne data alle stampe l'opera fondamentale di Beltrami, il Saggio di interpretazione della geometria non euclidea, che potete trovare integralmente qui.
Con tale opera, Beltrami mostrò che la geometria iperbolica è localmente la geometria di superfici a curvatura costante negativa dette superfici pseudosferiche.
Riporto uno splendido passo illustrante gli studi di Beltrami tratto dal libro Una via di fuga di Piergiorgio Odifreddi:
"Il suo Saggio di interpretazione della geometria non euclidea costituisce l'altra faccia della medaglia dell'indipendente lavoro di Riemann del 1854. Entrambi furono pubblicati molto tempo dopo essere stati scritti. Entrambi contenevano molte idee innovative e feconde...Beltrami inizia considerando una pseudosfera...Per calcolare la curvatura della pseudosfera in un punto, bisogna considerare le sezioni perpendicolari al piano tangente. Quella di minima curvatura è la trattrice. Quella di massima curvatura un ovale, rivolto nella direzione opposta. Dunque, le curvature estreme delle sezioni hanno segni contrari, e la curvatura della pseudosfera è negativa. Inoltre, i raggi di curvatura della trattrice (rt) e dell'ovale (r₀) costituiscono le proiezioni sull'ipotenusa dei cateti di un triangolo rettangolo, che ha per altezza la lunghezza della corda che definisce la trattrice (r)."
Interrompiamo un attimo lo stralcio del testo di Odifreddi, ricordando un famosissimo teorema geometrico, utile per capire il seguito della narrazione del matematico: il secondo teorema di Euclide.
Esso afferma che, in un triangolo rettangolo, l'altezza relativa all'ipotenusa è medio proporzionale tra le proiezioni dei 2 cateti sull'ipotenusa, come illustrato nel seguente video:
Praticamente, nel nostro caso, abbiamo la seguente relazione:

Da cui si ricava facilmente che:

Riporto il seguito del passo dal libro Una via di fuga:
"Dunque, la curvatura della pseudosfera è costante e pari a -1/r². La pseudosfera deriva appunto il suo nome dal fatto di avere la stessa curvatura costante della sfera, però con segno opposto. Le analogie non si limitano alla curvatura. Ad esempio, la superficie della pseudosfera è 4πr², come per la sfera. E il suo volume 2πr³/3, come per la semisfera. Ma c'è una differenza cruciale: mentre la sfera è un modello completo della geometria sferica, la pseudosfera è solo un modello parziale della geometria iperbolica. Da questo punto di vista la pseudosfera assomiglia, più che a una sfera, a un cono. Entrambe le superfici corrispondono infatti a settori circolari dei rispettivi piani: in particolare, la pseudosfera a un settore di orociclo [curva del piano iperbolico perpendicolare a tutte le rette appartenenti ad un fascio].
 |
| Orociclo blu nel disco di Poincaré e alcune rette ortogonali rosse |
Questa duplice natura della pseudosfera si può sintetizzare in una doppia proporzione:
La rappresentazione pseudosferica del piano iperbolico, oltre a essere incompleta, è anche imperfetta. Anzitutto, ha un buco, che deriva dal fatto che la trattrice ha un asintoto. E poi, ha una piega sul bordo che unisce le sue 2 parti. Questa piega deriva, a sua volta, dalla corrispondente piega che la trattrice ha nel punto che corrisponde all'inizio della trazione, e separa il movimento nelle 2 direzioni. Beltrami cercò di ovviare al problema, costruendo un modello di carta che si può estendere a piacere. Egli partì dall'osservazione che, per ottenere un punto iperbolico isolato, basta prendere un cerchio di carta e tagliarlo a spicchi come una torta. Eliminando spicchi alterni, e unendo i rimanenti, si ottiene una porzione di superficie sferica. Aggiungendo invece spicchi alterni, e inserendoli tra quelli di partenza, si ottiene una porzione di superficie iperbolica. Per ottenere una superficie iperbolica intera, Beltrami tagliò delle striscioline di carta ad arco di cerchio, tutte con lo stesso raggio r e la stessa altezza. E le incollò insieme in modo da far aderire il lato interno di una con quello esterno dell'altra. Minore è l'altezza delle striscioline, e migliore è l'approssimazione al piano iperbolico con raggio di curvatura r.
Le striscioline corrispondono a orocicli equidistanti fra loro, e costituiscono una griglia analoga ai paralleli di una sfera. Poiché il loro lato interno è leggermente più curvo di quello esterno, i loro bordi non combaciano perfettamente: questo crea una curvatura negativa costante della superficie, e fa sì che il modello appaia tutto ondulato. Quand'esso è arrotolato, si presenta come un segmento di pseudosfera con il bordo ondulato, appunto, e all'epoca un giornale satirico lo paragonò alla "cuffia di una nonna". Di qui, il nome di cuffia di Beltrami."
Esiste inoltre un importante teorema valido per la sfera che si può estendere alla pseudosfera: il teorema di Gauss-Bonnet.
Sappiamo che in una sfera è valida la relazione:
dove α, β, γ indicano gli angoli del triangolo sferico (la cui somma è maggiore di 180°) e R il raggio della sfera.
Sappiamo però che la sfera ha curvatura K = 1/R²; ergo, possiamo riscrivere la relazione precedente come:
Il bello è che tale risultato è valido per qualsivoglia superficie di curvatura costante.
Trattasi della formula di Gauss-Bonnet, enunciata in primis da Gauss nell'opera Disquisitiones generales circa superficies curvas (1827) ed estesa dal matematico francese Pierre Ossian Bonnet (1819-1892).
Essa si può persino generalizzare non soltanto a triangoli, ma pure a poligoni su superfici non necessariamente a curvatura costante.
Se riprendiamo la pseudosfera, assumendo per semplicità che essa abbia un raggio unitario, la sua curvatura è pari a K = -1.
Adesso, applicando la formula di Gauss-Bonnet, otteniamo:

Ne consegue che sulla pseudosfera la somma degli angoli interni di un triangolo è minore di 180° e il difetto risulta equivalente all'area del triangolo, in consonanza col fatto che la pseudosfera è una superficie iperbolica.
Da ciò deriva un fatto ancora più stupefacente: l'area di un triangolo è:
che è minore o uguale a π.
Dunque sulla pseudosfera non può esistere un triangolo avente un'area superiore a π, seppur possano esistere triangoli con perimetro infinito!
Ed ora un fantastico video sulla trattrice e la pseudosfera:
Una lettura molto interessante sull'argomento che vi consiglio caldamente è sicuramente quella dell'articolo "Di trattrici e pseudosfere" di Gianluigi Filippelli sul blog Dropsea.
Ora abbandoniamo la pseudosfera per andare a scoprire brevissimamente un altro oggetto geometrico alquanto singolare: la sfera cornuta di Alexander.
La sfera di Alexander è un eccezionale esempio di superficie fortemente convoluta ed intrecciata, tanto da essere complicato individuare a vista un interno e un esterno.
Introdotta nel 1924 da James Waddell Alexander (1888-1971), professore di matematica all'Università di Princeton e successivamente all'Institut for Advanced Studies, la sfera cornuta è costituita da una successione di paia di corna, che risultano intrecciate fra loro e le cui estremità tendono ad avvicinarsi progressivamente.
Per immaginare come dar vita a una figura così complessa ed articolata, provate ad utilizzare le dita della mano.
Avvicinate pollice e indice di una mano, dopodiché lasciate campo libero alla vostra fantasia, immaginando che un pollice ed un indice più piccoli crescano alle loro estremità, continuando all'infinito tale "germogliazione".
La figura geometrica che ne risulta è un frattale (di frattali abbiamo parlato qui), formato da coppie di "dita" che si intrecciano, delineando circonferenze aperte perpendicolari di raggio sempre più minuscolo.
Sebbene appaia come un oggetto assai strambo e complesso, la sfera di Alexander (assieme al suo interno) risulta omeomorfa a una sfera.
In parole semplici, 2 oggetti geometrici si dicono omeomorfi se il primo può essere trasformato nel secondo, tirandolo e piegandolo.
Se non avete ben compreso il concetto di omeomorfismo, osservate la seguente animazione in cui una tazza muta in una ciambella (in matematica viene chiamata toro) e viceversa:
Pertanto, una sfera cornuta può essere deformata sino a trasformarsi in una tradizionale sfera, senza che sia necessaria bucarla oppure romperla.
Per concludere, un simpatico disegno di Simon Fraser raffigurante il noto matematico britannico John Horton Conway avente in testa la sfera cornuta di Alexander:

Come ciliegina sulla torta, dato che abbiamo lungamente parlato di sfere, tradizionali e non, vi riporto il meraviglioso Valzer Op. 235 di Josef Strauss, noto anche con l'appellativo "Music of the Spheres":
-----------------------------------------------------------------------------------------
Fonti principali:
- Il lungo racconto dell'origine di Margherita Hack, Walter Ferreri, Guido Cossard
- Dalla geometria di Euclide alla geometria dell'Universo di Ferdinando Arzarello, Cristiano Dané, Laura Lovera, Miranda Mosca, Nicoletta Nolli, Antonella Ronco
- Una piramide di problemi di Claudio Bartocci
- Una via di fuga di Piergiorgio Odifreddi
- Il libro della Matematica di Clifford A. Pickover




.gif)
.gif)
.gif)
.gif)
















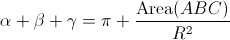























Caro Leonardo, mi sono perso nel tuo post incredibile e ricchissimo per un bel pezzo! E' stato un viaggio molto affascinante, un po' come farsi il giro dentro la sfera cornuta di Alxander.
RispondiEliminaNe voglio una!!
:-)
Grazie mille, Spartaco!!!
EliminaE' stato un post che ha richiesto vari giorni per essere portato a termine, ma avevo proprio voglia di descrivere questi oggetti geometrici così affascinanti e dalle incredibili peculiarità. E poi, quale miglior momento per elaborare ciò, considerato l'imminente Carnevale della Matematica dal tema "Matematica: che palle!"? ;)
Come spesso accade, c'è da dedicare un po' di tempo ai tuoi articoli, ma alla fine ne vale sempre la pena. Ottimo e abbondante.
RispondiEliminaUn saluto
PS:
E' una mia opinione e quindi vale praticamente zero, ma mi sembra che i tuoi articoli i cui contenuti sono sempre di elevata qualità, forse "meriterebbero" una rivisitazione del contenitore (template ed altro). Hai mai pensato a un restyling del blog?
Grazie dell'apprezzamento, Marco!
EliminaPer quanto riguarda un possibile restyling del blog, potrei certamente effettuare qualche modifica in futuro, qualcosa che però non snaturi completamente il look di questo blog!
Voglio precisare che il look è importante ma sicuramente secondario rispetto ai contenuti e poi è un fattore soggettivo. Quello che cercavo di dire è che contenuti così "importanti" potrebbero essere esaltati o, al contrario, perdere di impatto se il look non è adeguato. Sai meglio di me che anche l'occhio vuole la sua parte ed il rischio è che l'eventuale nuovo lettore (quello che ancora non ti conosce) possa avere una prima impressione che lo porti a conclusioni errate rispetto alla qualità dei contenuti. In concreto ci sono cosette che potrebbero essere migliorate o sistemate sempre e solo con l'obbiettivo di dare maggiore "importanza" ad un ottimo blog come il tuo che parla di scienza (e musica). Sono sicuro che comprendi benissimo il mio intento che non è affatto critico bensì costruttivo e che mi deriva da una sorta di deformazione visto che di blog ne vedo tanti e molti li ho anche "sistemati ed ottimizzati" per qualche amico.
EliminaMi sono permesso di esprimere il mio parere (che, ripeto, vale ben poco) perché sono certo che comprendi le mie buone intenzioni vista l'alta considerazione che ho dei tuoi articoli. Se vuoi (in privato; puoi contattarmi via mail) posso scriverti nello specifico cosa vedo "migliorabile" soprattutto nell'usabilità del blog.
Un saluto e scusa se mi sono permesso, ma sono fatto così, dico quello che penso soprattutto se so che dall'altra parte ho persone di cui ho un'alta considerazione; non m mi esprimo se non ne vale la pena.
Marco, sono sempre lieto quando arriva un commento costruttivo come il tuo. Sono inoltre lusingato dalla tua alta considerazione nei miei confronti.
EliminaCome ho già detto, mi piacerebbe in futuro effettuare un piccolo restyling del blog, a patto che sia qualcosa che lo valorizzi e non gli faccia perdere il suo "stile" non serioso. Accetto volentieri di leggere i tuoi preziosi suggerimenti.
Ti contatto via mail. Grazie ancora e un salutone!!!