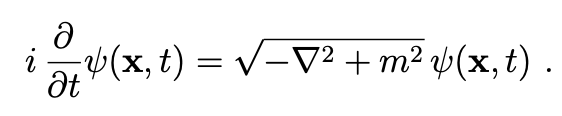Partiremo con una breve premessa un po' tecnica, dopodiché prometto che la narrazione diventerà molto più fruibile anche per il lettore non avvezzo al formalismo matematico della meccanica quantistica e della relatività ristretta.
È ben noto che l'equazione fondamentale alla base della meccanica quantistica è l'equazione di Schrödinger (ne abbiamo parlato qui e qui)
qui scritta per particella libera (ossia in assenza di potenziale) e assumendo l'uso di unità naturali, cioè ponendo $\hbar = 1$.
Ovviamente più in generale possiamo scriverla come
$i \frac{\partial}{\partial t} | \psi (t) \rangle = H | \psi(t) \rangle$,
ove $H$ denota l'hamiltoniana di una particella libera non relativistica, ovvero
$H = \frac{\mathbf{p}^2}{2m}$.
Detto ciò, una domanda lecita sarebbe chiedersi come sia possibile estendere l'equazione di Schrödinger al caso di una particella relativistica.
Ciò che immediatamente si può fare è scrivere l'hamiltoniana grazie alla relazione di dispersione relativistica
$H = \sqrt{\mathbf{p}^2 + m^2}$,
dove abbiamo imposto, per via delle unità naturali, la velocità della luce $c = 1$ (non utilizzando le unità naturali la relazione sarebbe stata $H = \sqrt{c^2 \mathbf{p}^2 + c^4 m^2}$).
Se si andasse ad utilizzare questa nuova $H$ all'interno dell'equazione di Schrödinger si otterrebbe:
Trattasi di un'espressione problematica per essere una relazione relativistica dato che le derivate spaziali e temporali sono di ordine diverso e ciò non la rende invariante di Lorentz.
Per cercare di risolvere il problema, ossia cercare di rendere quantomeno uguale l'ordine delle derivate temporale e spaziale, possiamo provare ad applicare il termine $i \frac{\partial}{\partial t}$ a tutta l'equazione precedente, il che conduce all'espressione
Trattasi della cosiddetta equazione di Klein-Gordon (proposta da Oskar Klein e Walter Gordon nel 1926) per la funzione d'onda $\psi(\mathbf{x},t)$, equazione che risulta consistente con la relazione di dispersione relativistica se compiamo le seguenti identificazioni:
in cui ovviamente $H$ e $\mathbf{p}$ sono rispettivamente l'operatore hamiltoniano e l'operatore momento.
Un ultimo piccolo importante step da compiere è usare le seguenti relazioni
le quali ci permettono di scrivere l'equazione di Klein-Gordon nella sua forma covariante (per i pignoli, abbiamo assunto la convenzione "mostly minus" del tensore metrico $\eta^{\mu \nu}$ dello spazio-tempo di Minkowski):
L'equazione così scritta è invariante di Lorentz in modo esplicito, dato che $\psi(\mathbf{x},t)$ ed $m$ sono scalari, mentre $\partial_{\mu} \partial^{\mu} = \frac{\partial^2}{\partial t^2} - \nabla^2 \equiv \partial^2 \equiv \Box$, cioè l'operatore dalembertiano, è uno scalare di Lorentz in quanto prodotto scalare di quadrivettori.
Detto ciò, l'equazione di Klein-Gordon continua ad avere dei problemi.
Innanzitutto $|\psi(\mathbf{x},t)|^2$, ovvero la densità di probabilità in meccanica quantistica, non è conservata (cioè non è indipendente dal tempo) giacché abbiamo ben 2 derivate temporali nell'equazione di Klein-Gordon.
L'equazione di Klein-Gordon non può oltretutto descrivere particelle aventi spin e presenta anche stati ad energia negativa come soluzioni, il che implicherebbe densità di probabilità negative, assolutamente non consistenti con l'interpretazione probabilistica tipica della meccanica quantistica non relativistica.
Insomma, sarebbe decisamente sbagliato considerare l'equazione di Klein-Gordon come un'equazione di Schrödinger relativistica; quella di Klein-Gordon è semplicemente un'equazione d'onda relativistica!
Tale problematica venne affrontata nientemeno che dal mitico Paul Adrien Maurice Dirac (1902-1984), il quale riuscì nell'impresa di pervenire, nel 1928, ad un'equazione, la famosa equazione di Dirac (di seguito scritta in forma covariante)
che presenta derivata spaziale e temporale entrambe del 1° ordine.
Tale equazione è tuttavia valida per gli spinori, non per funzioni d'onda scalari e, in particolare, serve a descrivere le particelle con spin semi-intero chiamate fermioni (tra cui troviamo anche l'elettrone e il positrone).
Non entreremo nel dettaglio della spiegazione di tale equazione, che andrebbe ben al di là degli scopi di questo post (gli interessati possono trovare una spiegazione già in alcuni testi della bibliografia in fondo al post).
Prima però di capire come tutto questo si ricolleghi alla scoperta del positrone voglio sottolineare il fatto che negli ultimi anni sia uscita una certa moda che consiste nel tatuarsi sul corpo l'equazione di Dirac e denominarla come "formula dell'amore".
Il problema sta nel fatto che non solo la suddetta equazione non ha nulla a che vedere con l'amore (magari già il bizzarro concetto quantistico di entanglement avrebbe leggermente più senso in tal direzione), ma spesso viene pure scritta in modo totalmente sbagliato, cioè per esempio come segue.
In questo caso non solo è chiaramente sbagliato l'utilizzo del segno +, ma c'è pure un dettaglio non da poco che manca: la slash notation.
Quella barretta che risulta inserita nella vera equazione di Dirac non è infatti messa lì a caso, come fosse una trollata da parte dei fisici per complicare la vita dei poveri mortali, ma ha un significato ben preciso che coinvolge le cosiddette matrici gamma.
Insomma, se proprio volete tatuarvela, vi consiglio di tatuarvi quella giusta per non farvi prendere in giro da coloro (seppur pochi 😉) che conoscono davvero l'equazione di Dirac.
Tornando alle cose serie, vi starete giustamente chiedendo a cosa sia servita tutta questa piuttosto pesante premessa.
Essa è servita in primis per farvi capire come non sia banale considerare assieme la meccanica quantistica e la relatività speciale (non mettiamo poi nel calderone la relatività generale, la cui unificazione con la meccanica quantistica è un problema ancora apertissimo in fisica).
Infatti spesso quando si parla di meccanica quantistica + relatività speciale ci si riferisce ad una teoria nota come teoria quantistica dei campi o, in inglese, quantum field theory (abbreviata QFT).
Ecco, se pensate che la meccanica quantistica sia qualcosa di molto complesso, la QFT rappresenta un netto ulteriore step in complessità, oltre a costituire un vero e proprio framework per la fisica moderna ed essere la base teorica della fisica delle particelle.
La premessa è servita poi per farvi quantomeno comprendere perché, nella storia della fisica moderna, non è stata sufficiente l'introduzione dell'equazione di Klein-Gordon e fu necessario il geniale contributo di Dirac per poter compiere giganteschi passi avanti nel tentativo di fusione tra meccanica quantistica e relatività ristretta.
Il nocciolo della questione viene in particolare dal fatto che, così come l'equazione di Klein-Gordon, pure quella di Dirac ammette soluzioni con energie negative!
Ciò implicherebbe la non esistenza di uno stato fondamentale (ground state) del sistema, poiché le particelle tenderebbero sempre a preferire di dirigersi verso stati ad energia negativa.
Oltretutto, tenendo conto che l'equazione di Dirac descrive i fermioni, e i fermioni sono quelle particelle che debbono obbedire al noto principio di esclusione di Pauli (leggete qui), si potrebbe supporre (come fece Dirac) che tutti gli stati ad energia negativa siano occupati, ossia che sussista il cosiddetto "mare di Dirac" inaccessibile alle particelle con energia positiva a causa del principio di Pauli.
Ecco un'immagine illustrativa della situazione tratta dal testo Particle Physics di Martin e Shaw.
Sarebbe tuttavia chiaramente possibile eccitare (in qualche modo) una particella situata nel mare infinito di Dirac delle energie negative verso la regione delle energie positive, totalmente vuota.
Il risultato sarebbe avere una buca nel mare di Dirac, tecnicamente (nel linguaggio tipico della fisica dei semiconduttori) una lacuna (in inglese hole), come ben mostra la seguente immagine.
 |
| Fonte: https://oer.physics.manchester.ac.uk/NP/Notes/Notes/Notesse28.xht |
Tale lacuna (il pallino bianco della figura) è sostanzialmente un'antiparticella, cioè, in parole povere, una particella che presenta la medesima massa (ed altre proprietà) della particella originaria ma carica elettrica opposta.
Quando una particella e un'antiparticella interagiscono avviene il fenomeno dell'annichilazione, che dà luogo a particelle più leggere con rilascio di energia.
L'antiparticella dell'elettrone $e^-$ è proprio il positrone $e^+$; le 2 particelle interagiscono nello specifico a bassa energia secondo questa relazione:
L'introduzione del concetto di antiparticella rimase un puro risultato teorico proprio sino alla scoperta sperimentale del positrone. Entriamo ora finalmente nei meandri dell'interessante storia inerente alla suddetta scoperta.