Trattasi di un fenomeno poco conosciuto inerente alla meccanica dei fluidi.
Immaginiamo di voler determinare il flusso a bassa velocità di un fluido pressoché incomprimibile attorno ad un cilindro.
Ricordo che il flusso, in parole semplicissime, è la quantità di una grandezza (ad esempio, la massa o il calore) che attraversa una certa superficie nell'unità di tempo.
Nel post "Il campo gravitazionale: il teorema di Gauss" abbiamo analizzato, per esempio, il flusso del campo gravitazionale.
Cosa significa invece fluido incomprimibile (o incompressibile)?
Per chi non lo sapesse, significa semplicemente che applicando una certa pressione sulla sua superficie il volume rimane inalterato.
Un esempio di fluido incomprimibile è l'acqua.
Esiste il famoso esperimento della siringa, utile per spiegare l'incompressibilità dell'acqua.
Prendete una siringa (senza ago) e inserite al suo interno un po' d'acqua.
Dopodiché tappate il foro con una mano e spingete con l'altra mano il pistone della siringa.
Noterete che anche applicando sullo stantuffo una grande forza, non riuscirete in alcun modo a far diminuire il volume (o, analogamente, la densità) dell'acqua.

Prima di arrivare a trattare le peculiarità del flusso di un fluido incompressibile intorno a un cilindro (e di introdurre i vortici di von Kármán), dobbiamo fare altre premesse di fondamentale importanza.
Innanzitutto, ricordo che una caratteristica chiave dei fluidi è, oltre la loro densità, anche la viscosità.
La viscosità è una grandezza che specifica la resistenza di un fluido allo scorrimento, quindi rappresenta una misura della capacità di un fluido di fluire liberamente.
 |
| Fluidi a bassa viscosità (in alto) e ad alta viscosità (in basso) |
Densità e viscosità distinguono i fluidi in 2 categorie:
1) fluidi ideali: hanno densità costante e viscosità pari a 0.
2) fluidi reali: presentano un valore di viscosità diverso da 0.
I fluidi ideali sono, come fa capire il nome stesso, un caso limite dei fluidi reali.
La tipologia di fluidi che ci interessa in questo contesto è sicuramente quella dei fluidi reali, cioè quella in cui rientrano tutti i fluidi che si trovano in natura (anche se alcuni, come l'acqua, si avvicinano molto al modello utopico di fluido ideale).
È necessario affermare che quando il moto di fluidi reali avviene a bassa velocità, allora il moto si dice laminare.
In effetti, a basse velocità, la presenza di viscosità implica che i vari "filetti" fluidi in cui si può immaginare decomposto il tubo (per il momento supponiamo appunto che il fluido scorra dentro un tubo e non intorno ad un cilindro chiuso) scorrono gli uni sugli altri con velocità diverse.
In particolare, i "filetti" fluidi rimangono sempre paralleli tra loro, alla stregua di minuscole "lamine" tutte parallele, da cui deriva la definizione di moto laminare.
 |
| Esempio di flusso laminare |
Come potete riscontrare dall'animazione appena riportata, la velocità del fluido aumenta avvicinandosi all'asse del condotto.
La velocità è appunto massima sull'asse del tubo.
Supponiamo ora che il moto laminare avvenga in un tubo cilindrico di raggio R.
Ipotizzando questo condotto disposto in maniera orizzontale, lungo l e con una differenza di pressione p₁ - p₂ agli estremi, allora valgono le osservazioni che seguono.
OSSERVAZIONE N.1:
Il modulo della velocità del fluido varia con il raggio r dello strato cilindrico, cioè con la distanza dall'asse, in accordo con la seguente formula:
.gif)
dove la lettera greca η (eta) indica la viscosità del fluido.
La velocità massima si ottiene quando r = 0, e vale:
.gif)
mentre la velocità minima si ottiene per r = R, alla parete del tubo, e vale semplicemente:
.gif)
OSSERVAZIONE N.2:
La portata q (ovvero la quantità di fluido che attraversa una sezione di area S del condotto nell'unità di tempo) è definita dalla cosiddetta legge di Hagen-Poiseuille (ricavata sperimentalmente, in modo indipendente, da Gotthilf Heinrich Ludwig Hagen, nel 1839, e da Jean Louis Marie Poiseuille, nel 1838):
.gif)
Siccome la portata è definita pure come il prodotto tra l'area di una sezione del condotto e la media delle velocità vm nei vari punti della sezione (una media spaziale, non temporale), ovvero
.gif)
allora, dato che nel nostro caso il condotto è cilindrico (quindi l'area di una sezione è semplicemente l'area del cerchio di raggio R), la portata si potrà esprimere come:
.gif)
da cui:
.gif)
Sostituendo a q la definizione fornita dalla legge di Hagen-Poiseuille si ottiene che la velocità media è data dall'uguaglianza:
.gif)
Tutto ciò implica che:
.gif)
Pertanto, per mantenere il flusso di fluido nel tubo è necessaria una differenza di pressione, ossia una forza sufficiente a vincere la resistenza al moto dovuta all'attrito interno (direttamente proporzionale alla viscosità).
A proposito di portata, vi consiglio di leggere un ottimo post di Sandro Ciarlariello sul suo blog Quantizzando (cliccate qui).
La legge di Hagen-Poiseuille risulta sempre verificata quando il raggio del condotto è assai piccolo.
Le cose cambiano per raggi più grandi.
Infatti, sussiste un valore critico della velocità oltre il quale appaiono dei vortici nel fluido e si parla dunque di moto turbolento o vorticoso.
I meccanismi che comportano la creazione di vortici sono legati a notevoli variazioni di velocità perpendicolarmente alle linee di corrente.
Inoltre, più aumenta la velocità, maggiori sono le forze di attrito interno tra i "filetti" di fluido.
Il fisico e ingegnere inglese Osborne Reynolds (1842-1912), nel 1883, dimostrò sperimentalmente che, per un condotto cilindrico, la transizione dal regime laminare a quello vorticoso avviene quando il parametro adimensionale
.gif)
chiamato, in suo onore, numero di Reynolds (Re), ha il valore 2000.
Specifichiamo che la lettera greca ρ (rho) designa la densità del fluido.
Possiamo ora finalmente tornare al problema di partenza, ovvero cosa succede quando c'è un flusso, a piccola velocità, di un fluido non dentro un tubo cilindrico ma attorno ad un cilindro.
Innanzitutto, possiamo dire che quando il numero di Reynolds è veramente molto piccolo (di poche unità al massimo), il flusso è del tutto stazionario.
Che significa?
Semplicemente che la velocità del fluido è costante in ogni punto e il flusso gira attorno al cilindro.
 |
| Flusso a bassa velocità intorno a un cilindro |
Se la velocità del fluido comincia ad aumentare, alzando di conseguenza il numero di Reynolds, il flusso appare differente.
Per valori del numero di Reynolds ancora abbastanza bassi si ha una circolazione dietro al cilindro, con la presenza di un paio di vortici.
Il flusso cambia nuovamente quando si arriva al numero 40 circa, anzi, muta totalmente.
Infatti, uno dei vortici dietro al cilindro diviene così lungo da rompersi e andarsene con la corrente del fluido.
Dopodiché il fluido si piega ad anello dietro al cilindro e genera un nuovo vortice.
Questi particolari vortici si staccano alternativamente dai 2 lati e vengono chiamati appunto vortici di von Kármán, mentre la corrente di vortici viene detta scia di von Kármán.
Quando il numero di Reynolds diventa mostruosamente elevato, allora si entra in pieno regime turbolento, dove tutto è caotico e irregolare.
Ecco 2 immagini illustrative dei vari casi di flusso analizzati:
 |
| Immagine 1 |
 |
| Immagine 2 |
Diciamo qualcosa in più ovviamente sui vortici di von Kármán.
Essi devono la propria denominazione al fisico ungherese Theodore von Kármán (1881-1963), che, nel 1911, sfruttando gli "strumenti" dell'analisi matematica, studiò l'esistenza di una fonte di resistenza aerodinamica che si verifica quando il flusso d'aria si separa da una superficie aerodinamica (un cilindro o comunque un corpo tozzo) e scivola ai suoi lati, avvolgendosi a spirale in 2 flussi paralleli di vortici.
L'intervallo di numeri di Reynolds in cui tali spettacolari vortici possono manifestarsi dipende dalla forma e dalle dimensioni del corpo che innesca il fenomeno, nonché dalla viscosità del fluido.
I vortici vengono talvolta osservati nei corsi d'acqua a valle dei pilastri cilindrici a sostegno dei ponti o nei piccoli movimenti circolari delle foglie cadute a terra quando un'auto vi passa accanto.
Alcune loro stupende manifestazioni si possono ammirare nella configurazione delle nuvole che si formano quando intercettano colossali ostacoli sulla Terra, ad esempio, un'elevata isola vulcanica.

I vortici di von Kármán possono essere davvero molto spettacolari ma anche pericolosi.
Come conseguenza della formazione di un vortice si ha infatti una modificazione della distribuzione delle pressioni attorno al corpo.
Una formazione alternata di vortici genera forze variabili periodicamente e quindi una vibrazione del corpo.
Nel caso in cui la frequenza di formazione dei vortici si avvicini alla frequenza naturale di vibrazione del corpo si ha il fenomeno della risonanza del medesimo.
Degli esempi sono dati dalla vibrazione dei cavi telefonici, dalla fluttuazione delle finestre avvolgibili (le veneziane) quando il vento le attraversa, ecc.
Una conseguenza catastrofica dei vortici è stata certamente l'incredibile crollo, il 7 novembre del 1940, del ponte sul fiume Tacoma, negli Stati Uniti, in seguito all'oscillazione del piano stradale.
Per un approfondimento su tal vicenda, cliccate qui.
Il fenomeno della scia vorticosa di von Kármán deve inoltre essere preso in considerazione in fase di progettazione di strutture come i periscopi per sottomarini, le ciminiere industriali e le antenne delle automobili.
Nel caso di un corpo cilindrico, la frequenza di formazione dei vortici è fornita dalla formula che segue:

dove:
- f indica la frequenza di distacco dei vortici;
- d è il diametro del cilindro;
- V designa la velocità del fluido a monte del cilindro;
- Re rappresenta ovviamente il numero di Reynolds.

viene spesso chiamato numero di Strouhal, dal nome del fisico ceco Vincent Strouhal, il primo ad investigare, nel 1878, sulla vibrazione dei cavi telefonici.
Concludiamo la narrazione con un aneddoto.
Von Kárman si riferì alla sua teoria come alla "teoria il cui nome ho l'onore di portare" poiché, secondo István Hargittai (professore di Chimica e autore del libro Martians of Science), "considerava la scoperta più importante dello scopritore.
Quando circa 20 anni dopo lo scienziato francese Henri Bénard reclamò la paternità della scoperta della scia vorticosa, von Kármán non protestò.
Con la sua caratteristica ironia, invece, propose che il termine scia vorticosa di Kármán venisse usato a Londra e che a Parigi si utilizzasse Boulevard d'Henri Bénard".
Per una trattazione maggiormente tecnica dei concetti descritti in questo post, potete vedere qui.
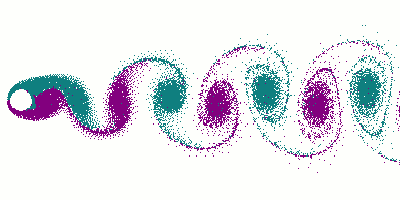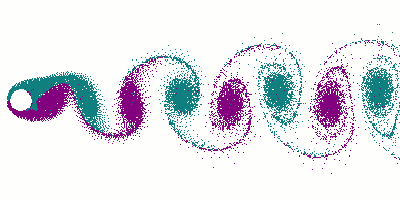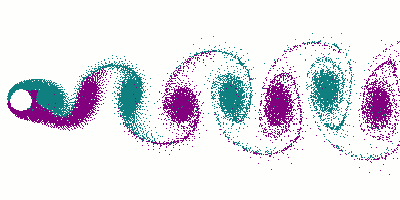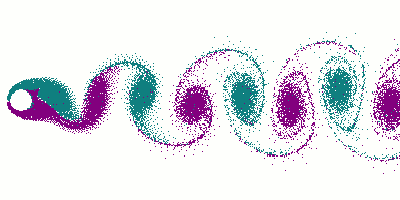


















Nessun commento:
Posta un commento