Ecco l'elenco delle puntate precedenti:
L'obiettivo del presente post è arrivare a derivare l'importante equazione di continuità.
Per far questo, cominciamo dicendo che, poiché $|\psi(\vec{r},t)|^2 \mathrm{d} \vec{r}$ rappresenta una probabilità, allora se noi andiamo ad integrare questa quantità su tutto lo spazio occorre che questa probabilità sia 1:
Non ha mai senso parlare infatti di una probabilità che superi 1, cioè il 100%.
La condizione ci fa anche capire che le funzioni d’onda devono essere necessariamente funzioni a quadrato sommabile.
Al tempo iniziale possiamo normalizzare all’unità la funzione d’onda, come appena detto.
Rimane un fattore di fase arbitrario che possiamo fissare a piacere perché, se mantenuto coerentemente, non avrà conseguenze fisiche.
Tuttavia, affinché tutto ciò sia coerente, è necessario che l’equazione di Schrödinger garantisca la normalizzazione nel futuro.
Se dovessimo infatti rinormalizzare la funzione d’onda ad ogni istante, l’equazione non sarebbe più soddisfatta!
Occorre pertanto che:
Andiamo a vedere se l’equazione di Schrödinger garantisce tale conservazione della norma. Partiamo dall’equazione di Schrödinger generale
e dalla sua forma complessa coniugata (quella dell'asterisco è un'altra notazione comune per indicarla)
Moltiplichiamo la prima per $\psi^*$ e la seconda per $\psi$, dopodiché sottraiamo. Ne risulta:
giacché
La norma risulta dunque conservata se vale
Scritta così potreste non aver capito molto, quindi cerchiamo di chiarire meglio cosa sia un operatore hermitiano, che è un concetto importantissimo ai fini della meccanica quantistica.
Se ricordate, qui avevamo introdotto il concetto di matrice hermitiana $H$, definendola come quella matrice quadrata in cui l'elemento nella $i$-esima riga e $j$-esima colonna è uguale al complesso coniugato dell'elemento nella $j$-esima riga e $i$-esima colonna (per tutti quanti gli indici $i$ e $j$).
Trattasi, in altre parole, di quella matrice che è sempre equivalente con la propria trasposta coniugata.
Avevamo considerato il seguente esempio di matrice hermitiana
che ci aveva permesso di comprendere immediatamente che gli elementi sulle diagonali sono numeri reali; se ci fossero numeri complessi sulle diagonali, non avremmo di fronte una matrice hermitiana!
Bene, il discorso per quanto riguarda gli operatori è sostanzialmente lo stesso.
Innanzitutto diciamo che la scrittura $\hat{H}^†$ denota il cosiddetto operatore aggiunto, il quale non è altro che una generalizzazione del concetto di trasposto coniugato.
Ergo, diciamo che un operatore $\hat{H}$ è hermitiano (o autoaggiunto) se è uguale al suo aggiunto, ossia, come abbiamo scritto prima, $\hat{H} = \hat{H}^†$.
Trattasi, in altre parole, di quella matrice che è sempre equivalente con la propria trasposta coniugata.
Avevamo considerato il seguente esempio di matrice hermitiana
Bene, il discorso per quanto riguarda gli operatori è sostanzialmente lo stesso.
Innanzitutto diciamo che la scrittura $\hat{H}^†$ denota il cosiddetto operatore aggiunto, il quale non è altro che una generalizzazione del concetto di trasposto coniugato.
Ergo, diciamo che un operatore $\hat{H}$ è hermitiano (o autoaggiunto) se è uguale al suo aggiunto, ossia, come abbiamo scritto prima, $\hat{H} = \hat{H}^†$.
Un aspetto molto importante da ricordare è che gli operatori hermitiani possono essere visti come l'analogo operatoriale dei numeri reali.
Dopo questa doverosa breve digressione, ci chiediamo ora se l’operatore hamiltoniano che abbiamo introdotto, cioè
Per capire ciò, andiamo a considerare l’integrando dell’espressione
e ci sostituiamo all'interno la definizione prima fornita di $\hat{H}$. Abbiamo nello specifico:
I 2 termini dell’energia potenziale si cancellano giacché si considera il potenziale sempre reale!
e ci sostituiamo all'interno la definizione prima fornita di $\hat{H}$. Abbiamo nello specifico:
In simboli: $V(\vec{r}) = V^*(\vec{r})$. Nello specifico, l’hamiltoniana è hermitiana quando il potenziale è reale.
Potenziali non reali comportano infatti la non conservazione della norma della funzione d’onda. Quello che resta è l’espressione
Nel nostro caso abbiamo:
Potenziali non reali comportano infatti la non conservazione della norma della funzione d’onda. Quello che resta è l’espressione
Andiamo ora a far uso del teorema di Green (sostanzialmente equivalente alla regola di Leibniz sulla derivata del prodotto di 2 funzioni), che ci dice che:
da cui
Nel nostro caso abbiamo:
Riprendiamo ora l’espressione riassuntiva
Dunque la derivata (rispetto al tempo) della densità locale + la divergenza della densità di corrente di probabilità è nulla.
La ragione del nome “equazione di continuità” diventa immediatamente palese quando si integri la formula su un volume finito $\Omega$.
Facendo ciò e ricordando che il teorema della divergenza asserisce che l’integrale, esteso ad un certo volume, della divergenza di un vettore eguaglia il flusso di tale vettore attraverso la superficie che delimita il volume considerato e che quindi vale la relazione:
dove $d \vec{S} = n̂ dS$, con n̂ versore normale, rivolto verso l’esterno, alla superficie $S_{\Omega}$ delimitante il volume $\Omega$.
Dall’equazione di continuità si ottiene facilmente
che è di interpretazione immediata.
Nel caso specifico dell’equazione di continuità associata all’equazione di Schrödinger, la sua forma integrata appena riportata ci dice che, se la probabilità di trovare nel volume $\Omega$ il sistema descritto dalla funzione d’onda $\psi(\vec{r},t)$ varia nel tempo, esiste un flusso di
probabilità che entra (se la derivata è positiva) o esce (nel caso opposto) da $\Omega$ attraverso la sua superficie, ma che all’interno del volume $\Omega$ non esistono né sorgenti né pozzi assorbenti di probabilità.
In parole povere, l'equazione di continuità assicura che $\rho$ possa cambiare solo a causa di un flusso entrante o uscente dalla regione di interesse e quindi la conservazione della norma avviene in modo continuo (cioè locale).
La ragione del nome “equazione di continuità” diventa immediatamente palese quando si integri la formula su un volume finito $\Omega$.
Facendo ciò e ricordando che il teorema della divergenza asserisce che l’integrale, esteso ad un certo volume, della divergenza di un vettore eguaglia il flusso di tale vettore attraverso la superficie che delimita il volume considerato e che quindi vale la relazione:
Dall’equazione di continuità si ottiene facilmente
Nel caso specifico dell’equazione di continuità associata all’equazione di Schrödinger, la sua forma integrata appena riportata ci dice che, se la probabilità di trovare nel volume $\Omega$ il sistema descritto dalla funzione d’onda $\psi(\vec{r},t)$ varia nel tempo, esiste un flusso di
probabilità che entra (se la derivata è positiva) o esce (nel caso opposto) da $\Omega$ attraverso la sua superficie, ma che all’interno del volume $\Omega$ non esistono né sorgenti né pozzi assorbenti di probabilità.
In parole povere, l'equazione di continuità assicura che $\rho$ possa cambiare solo a causa di un flusso entrante o uscente dalla regione di interesse e quindi la conservazione della norma avviene in modo continuo (cioè locale).
Naturalmente va detto che l'equazione di continuità non è peculiare della meccanica quantistica ma si ritrova anche nell'elettromagnetismo, dove $\rho$ e $\vec{j}$ denotano rispettivamente la densità di carica elettrica e la densità di corrente elettrica.
La medesima equazione si ritrova pure in idrodinamica, ove, nella descrizione del moto di un fluido, $\rho$ rappresenta la densità del fluido e $\vec{j}$ la densità della sua corrente.
Vediamo ora cosa succede considerando il semplice esempio di un’onda piana del tipo $\psi(\vec{r}) = A e^{i \vec{k} \cdot \vec{r}}$, quindi indipendente dal tempo.
Cos'è invece uno stato stazionario? Affidiamoci alla chiara definizione fornita da Wikipedia:
"In meccanica quantistica, uno stato stazionario è un autostato di un'hamiltoniana, o in altre parole, uno stato a energia fissata. È chiamato stazionario poiché il sistema, in assenza di perturbazioni esterne (termini ulteriori che si aggiungano all'hamiltoniano imperturbato del sistema), permane indefinitamente nello stato. Pertanto, un sistema che si trovi su uno stato stazionario, non è soggetto a cambiamento o a decadimento verso altri stati. L'energia del sistema è conservata in assenza di perturbazioni esterne.
Qualora a una certa energia siano presenti più stati stazionari, tali stati sono detti degeneri ".
Come si nota dal caso dell’onda piana, essa è uno stato perfettamente stazionario e appunto porta corrente.
Ne consegue che la corrente non c’è quando la funzione d’onda è fornita da una funzione reale, la quale descrive, come dicevamo, uno stato legato.
Uno stato legato è certamente anche uno stato stazionario, ma non tutti gli stati stazionari sono legati. In altri termini, gli stati legati formano un sottoinsieme degli stati stazionari.
Prendendo a riferimento l'atomo di Bohr, le orbite sono giustificate dal fatto che si suppone che gli elettroni vivano in stati stazionari, ma quelli sono, nel dettaglio, stati stazionari legati, ossia costretti a stare in uno spazio ristretto.
La medesima equazione si ritrova pure in idrodinamica, ove, nella descrizione del moto di un fluido, $\rho$ rappresenta la densità del fluido e $\vec{j}$ la densità della sua corrente.
Vediamo ora cosa succede considerando il semplice esempio di un’onda piana del tipo $\psi(\vec{r}) = A e^{i \vec{k} \cdot \vec{r}}$, quindi indipendente dal tempo.
Se andiamo ad applicare l’operatore densità di corrente a tale funzione d’onda, si ottiene:
come desideriamo che sia.
Un aspetto molto interessante da constatare della definizione di densità di corrente
Un aspetto molto interessante da constatare della definizione di densità di corrente
sta nel fatto che essa ci spiega perché è importante che la funzione d’onda, in generale, sia un’entità complessa.
Infatti $\vec{j}$ dipende essenzialmente dalla differenza $[\psi^* \nabla \psi - \psi \nabla \psi^*]$; quindi, se la funzione è reale (ed è possibile che sia reale), la densità di corrente è nulla, perché i 2 termini diventano uguali!
Ma in fisica, in generale, c’è una densità di corrente trasmessa e un’onda piana trasmette tranquillamente corrente.
È interessante chiedersi a questo punto quand’è che si hanno funzioni d’onda reali e che situazioni rappresentano.
La risposta è che una funzione d’onda reale rappresenta uno stato legato, non uno stato stazionario (indipendente dal tempo) generale. Uno stato legato non trasporta quantità di corrente, quantità di particella.
Per capire meglio cosa sia uno stato legato, riportiamo un breve passo dall'ottimo testo Introduzione alla meccanica quantistica di David J. Griffiths:
“In meccanica classica un potenziale unidimensionale indipendente dal tempo può dar luogo a 2 tipi di moto piuttosto diversi. Se $V(x)$ diventa più grande dell’energia totale della particella ($E$) da entrambe le parti dell’asse $x$, allora la particella è “intrappolata” dentro la buca di potenziale: rotola avanti e indietro tra i punti di inversione [turning points], ma non può fuoriuscire (ovviamente a meno che non le venga fornita energia extra, per esempio da un motore).
Chiamiamo un tale stato stato legato [bound state].
D’altra parte, se $E$ è maggiore di $V(x)$ da una o entrambe le parti, allora la particella arriva dall’“infinito”, rallenta o accelera sotto l’influenza del potenziale e se ne ritorna all’infinito. Essa infatti non può rimanere intrappolata nel potenziale a meno che non ci sia qualche meccanismo, come l’attrito, che dissipi energia.
Chiamiamo uno stato di questo genere stato di diffusione [scattering state].
Alcuni potenziali ammettono solo stati legati (per esempio quello dell’oscillatore armonico), altri solo stati di diffusione (un potenziale con un massimo senza minimi relativi, per esempio), altri ancora entrambi i tipi, a seconda dell’energia della particella.
[Considerando un potenziale all’infinito, si ha]:
Ma in fisica, in generale, c’è una densità di corrente trasmessa e un’onda piana trasmette tranquillamente corrente.
È interessante chiedersi a questo punto quand’è che si hanno funzioni d’onda reali e che situazioni rappresentano.
La risposta è che una funzione d’onda reale rappresenta uno stato legato, non uno stato stazionario (indipendente dal tempo) generale. Uno stato legato non trasporta quantità di corrente, quantità di particella.
Per capire meglio cosa sia uno stato legato, riportiamo un breve passo dall'ottimo testo Introduzione alla meccanica quantistica di David J. Griffiths:
“In meccanica classica un potenziale unidimensionale indipendente dal tempo può dar luogo a 2 tipi di moto piuttosto diversi. Se $V(x)$ diventa più grande dell’energia totale della particella ($E$) da entrambe le parti dell’asse $x$, allora la particella è “intrappolata” dentro la buca di potenziale: rotola avanti e indietro tra i punti di inversione [turning points], ma non può fuoriuscire (ovviamente a meno che non le venga fornita energia extra, per esempio da un motore).
Chiamiamo un tale stato stato legato [bound state].
D’altra parte, se $E$ è maggiore di $V(x)$ da una o entrambe le parti, allora la particella arriva dall’“infinito”, rallenta o accelera sotto l’influenza del potenziale e se ne ritorna all’infinito. Essa infatti non può rimanere intrappolata nel potenziale a meno che non ci sia qualche meccanismo, come l’attrito, che dissipi energia.
Chiamiamo uno stato di questo genere stato di diffusione [scattering state].
Alcuni potenziali ammettono solo stati legati (per esempio quello dell’oscillatore armonico), altri solo stati di diffusione (un potenziale con un massimo senza minimi relativi, per esempio), altri ancora entrambi i tipi, a seconda dell’energia della particella.
[Considerando un potenziale all’infinito, si ha]:
Nella “vita reale” la gran parte dei potenziali va a zero all'infinito, nel qual caso il criterio diventa ancora più semplice:
”
Vediamo una splendida immagine illustrativa tratta dalla versione inglese del libro sopracitato.
"In meccanica quantistica, uno stato stazionario è un autostato di un'hamiltoniana, o in altre parole, uno stato a energia fissata. È chiamato stazionario poiché il sistema, in assenza di perturbazioni esterne (termini ulteriori che si aggiungano all'hamiltoniano imperturbato del sistema), permane indefinitamente nello stato. Pertanto, un sistema che si trovi su uno stato stazionario, non è soggetto a cambiamento o a decadimento verso altri stati. L'energia del sistema è conservata in assenza di perturbazioni esterne.
Qualora a una certa energia siano presenti più stati stazionari, tali stati sono detti degeneri ".
Come si nota dal caso dell’onda piana, essa è uno stato perfettamente stazionario e appunto porta corrente.
Ne consegue che la corrente non c’è quando la funzione d’onda è fornita da una funzione reale, la quale descrive, come dicevamo, uno stato legato.
Uno stato legato è certamente anche uno stato stazionario, ma non tutti gli stati stazionari sono legati. In altri termini, gli stati legati formano un sottoinsieme degli stati stazionari.
Prendendo a riferimento l'atomo di Bohr, le orbite sono giustificate dal fatto che si suppone che gli elettroni vivano in stati stazionari, ma quelli sono, nel dettaglio, stati stazionari legati, ossia costretti a stare in uno spazio ristretto.
In altri termini, essi hanno dei nodi al termine di una certa regione spaziale (2 turning point), un po’ come una corda vincolata ad avere nodi ad entrambi i suoi estremi.
Per ora concludiamo qui la trattazione; segnaliamo sin da subito che per proseguire con le puntate sulla meccanica quantistica avremo prima bisogno di introdurre brevemente un concetto matematico a dir poco essenziale, la trasformata di Fourier, a cui dedicheremo prossimamente un post.
Per ora concludiamo qui la trattazione; segnaliamo sin da subito che per proseguire con le puntate sulla meccanica quantistica avremo prima bisogno di introdurre brevemente un concetto matematico a dir poco essenziale, la trasformata di Fourier, a cui dedicheremo prossimamente un post.
























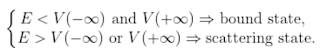



















Gentilissimo sig. Petrillo, ho apprezzato lo sforzo di divulgazione che sta facendo. Le faccio notare solo un paio di imprecisioni:
RispondiElimina1 - quando scrive l'integrale sul volume 3D le consiglio di usare un simbolo piu' preciso -- ad esempio d^3r -- e non il simbolo di r con il vettore (come nel teorema della divergenza). Inoltre nella prima parte (si veda l'integrale della valore assoluto della funzione d'onda) usa un simbolo diverso con r in neretto.
2 - nella dimostrazione della conservazione della probabilita' la derivata temporale prima d'integrale deve essere una derivata ordinaria e non parziale.
3 - aggiungerei anche per il simbolo del gradiente un piccolo vettore sopra al simbolo per indicare che e' un campo vettoriale e questo spiega meglio il significato del prodotto scalare nei vari passaggi e nella definizione della corrente di probabilita' come vettore.
4 - infine in alcune formule il simbolo di vettore e' leggermente spostato fuori del simbolo stesso.
5 - infine aggiungerei che gli autovalori di una matrice hermitiana sono reali e questo e' il punto importante.
Buona giornata. P A Grassi
Gentilissimo sig. Grassi, la ringrazio per il commento e per i suggerimenti forniti. Desidero però solo farle notare, per quanto concerne le sue giuste considerazioni sulla notazione utilizzata, che siamo su Blogger, un contesto non proprio ideale per una scrittura scientifica sempre perfetta. Inoltre l'uso di una shorthand notation si applica pure in contesti un po' più comodi di questo e il lettore medio credo mi perdonerà eventuali tipiche omissioni date per scontato o notazioni equivalenti ben note. Per quanto concerne la sua corretta considerazione circa gli autovalori, non l'ho menzionata perché il discorso autovalori e autofunzioni/autostati verrà affrontato in post successivi, dove quel punto da lei segnalato sarà sicuramente richiamato.
EliminaCordiali saluti.
Leonardo Petrillo