SOLUZIONE ALTERNATIVA AL QUESITO N.8 DELLA PROVA DI MATEMATICA P.N.I. DELL'ESAME DI STATO 2013

In questo post osserveremo una soluzione alternativa, rispetto a quelle diffuse nel web, del quesito n.8 della prova di matematica P.N.I. dell'esame di stato 2013.
Innanzitutto, ecco la traccia dell'esercizio:

Se ricordate, lo scorso anno avevamo risolto un quesito dell'esame che si basava proprio sul teorema del marchese de l'Hôpital (cliccate qui per rivedere quel post).
Quest'anno c'è stato un quesito simile, in cui, però, si richiede esplicitamente di non utilizzare il suddetto teorema.
Come si risolve allora il limite sopra riportato?
Sussistono diverse strade.
Come potete verificare qui, si può far ricorso alla definizione di derivata, oppure attuare una semplice sostituzione e sfruttare i limiti notevoli.
Esiste però un'ulteriore via di risoluzione, che non necessita di derivate, né (all'atto pratico) di limiti notevoli.
Ed è proprio quest'ultima che andremo ad illustrare.

Innanzitutto, osserviamo che abbiamo una forma indeterminata del tipo 0/0.
La traccia del quesito ci impedisce di applicare il teorema di de l'Hôpital, ma non vieta di andare a valutare il limite destro e il limite sinistro.
D'altronde, ciò risulta utile dato che una funzione ha limite in un punto x₀ se e solo se ha limite destro e sinistro, e, inoltre, questi 2 limiti risultano finiti e coincidenti.
Questo significa che, nel nostro caso, deve valere la seguente uguaglianza:

Non dobbiamo dunque far altro che dimostrare che i 2 limiti in questione sono finiti ed entrambi equivalenti a -1.
Iniziamo con il primo limite (limite destro).
Abbiamo che x tende a pi greco da destra, cioè tende a π⁺, una quantità appena più grande di π.
Ora osservate il grafico della funzione seno:

Come potete notare, quando x = π la funzione restituisce un valore pari a 0.
Se ora vi spostate a destra di π di una quantità infinitesima, ovvero "osservate" il punto x = π⁺, noterete che la funzione assume un valore leggermente più basso di 0, un valore che potremmo chiamare 0 - ε, con ε (lettera greca epsilon) piccolissimo.
Pertanto, quando andiamo a sostituire il valore π⁺ all'interno dell'espressione, ossia andiamo a calcolare il limite, otteniamo:




Diamo una giustificazione a tale scrittura.
Innanzitutto, la quantità x - π al denominatore dell'espressione iniziale si è trasformata in ε poiché, sostituendo π⁺ ad x, avevamo una sottrazione tra una quantità appena maggiore di pi greco (appunto π⁺) e pi greco stesso.
In altre parole, è come se avessimo scritto π⁺ come π + ε ed avessimo eseguito la suddetta sottrazione.
In secondo luogo, specifichiamo che



è diventato 1 poiché il seno di pi greco è 0, come abbiamo visto, e un qualunque numero (in tal caso il numero di nepero e) elevato a zero restituisce 1.
Ultima precisazione: abbiamo potuto scrivere



come



per 2 motivi:

N.1)

Ponendo π⁺ = π + ε, avevamo l'espressione:



la quale poteva essere sviluppata con la formula di addizione relativa al seno:

Ergo:

ovvero proprio



in quanto il coseno di pi greco è pari a -1.

N.2)

Abbiamo potuto scrivere



in quanto, come si suol dire, la funzione f(x) = sen x presenta lo stesso ordine di infinitesimo della funzione f(x) = x.
In parole povere, il seno tende a 0 alla stessa velocità con cui ci tende la bisettrice del 1° e 3° quadrante del piano cartesiano.

Bisettrice del 1° e 3° quadrante

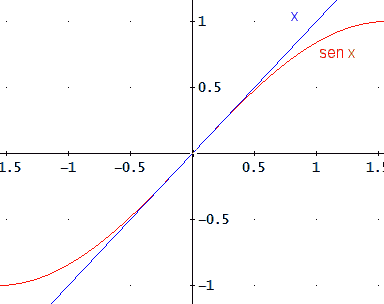
Tutto ciò è peraltro dimostrato pure dal più famoso tra i limiti notevoli:

Esso ci fa capire che per x abbastanza piccolo



come potete osservare nella seguente immagine:

Se non siete ancora convinti, basta ricordare lo sviluppo di Taylor-Maclaurin (centrato in x = 0) di sen x:





Esso, troncato al 1° ordine, ci fornisce un'ulteriore conferma del fatto che sen x = x.
Nel nostro caso abbiamo l'espressione



che, dopo tutte queste considerazioni, può essere vista alla stregua di ε, dato che esso è una quantità davvero infinitesimale, vicina allo zero o, in altre parole, uno 0⁺.
Per tutti questi motivi abbiamo quindi appurato che il nostro limite vale:

 


Ossia:




Abbiamo dimostrato che il limite destro vale proprio -1.
D'altronde:

Per chi desiderasse una prova di ciò, si può far riferimento allo sviluppo di Taylor-Maclaurin della funzione esponenziale:

il quale, troncato, ci fa capire che, per x piccolissimo



cosa che si può anche osservare nella seguente figura:

Nel nostro caso abbiamo tuttavia



Tale espressione si può scrivere, sfruttando lo sviluppo, come:



Poiché, ponendo t = -ε, avevamo che



e risostituendo si otteneva appunto:



Ciò va a confermare il fatto che:



Abbiamo pertanto calcolato il limite destro e osservato le giustificazioni che portano al risultato -1.
Ora focalizziamoci sul limite sinistro.
Dobbiamo dunque calcolare:






Il ragionamento è analogo a quello compiuto precedentemente.
La differenza è che qui abbiamo π⁻, ovvero una quantità leggermente più piccola di pi greco, cioè equivalente a π - ε, sempre con ε piccolissimo.
Adesso, riguardiamo il grafico della funzione seno:

  









Per un valore di x leggermente più piccolo di π, la funzione restituisce una quantità leggermente positiva, ossia 0 + ε.
Perciò, abbiamo:

Il denominatore è diventato negativo perché risultato di una differenza tra un valore leggermente più piccolo di pi greco (π⁻) e pi greco stesso.
Per le considerazioni effettuate in merito al limite destro, si può concludere che anche il limite sinistro risulta pari a:




Abbiamo pertanto dimostrato che:

cioè che:





Come volevasi dimostrare!