L'ultima volta abbiamo persino cercato di ricostruire l'affascinante storia di questa costante matematica.
Cosa ci sarà allora di nuovo da dire su tal numero?
In questo post andremo a scoprire il particolare metodo utilizzato nientemeno che da Isaac Newton, uno dei padri dell'analisi matematica, per determinare le cifre del pi greco.
Nel suo studio sulla emblematica costante, Newton prese in considerazione una semicirconferenza di centro C (1/2, 0) e raggio r = 1/2.
la quale, tenendo presente la figura sopra riportata, diviene:
Sviluppando i quadrati:
.gif)
da cui si ricava:
.gif)
ovvero l'equazione della semicirconferenza superiore.
Essa si può anche riscrivere nel seguente modo:
Newton prese in considerazione l'area A sottesa alla curva (nella figura, evidenziata in verde) tra x = 0 e x = 1/4.
Come ben noto, l'area sottesa a una certa curva si può esprimere attraverso un integrale definito.
In tal caso si ha:

Newton applicò il proprio teorema binomiale al fine di rendere l'espressione più maneggevole.
Cos'è il teorema binomiale?
Il teorema binomiale, detto anche formula di Newton, binomio di Newton o sviluppo binomiale, serve ad esprimere lo sviluppo della n-esima potenza (con n naturale) di un qualsivoglia binomio.
La formula è la seguente:
dove

è il cosiddetto coefficiente binomiale, che può essere esplicitato come segue:
.gif)
Proviamo a sviluppare ad esempio (a + b)⁴ mediante il teorema binomiale:
Esplicitando i coefficienti binomiali:
Ma se invece di avere un esponente naturale avessimo un esponente reale?
No problem, la formula di Newton si può generalizzare!
Il coefficiente binomiale diventa:
dove α è un numero reale e k un naturale.
La formula generalizzata è invece:
.gif)
L'ultimo termine è una quantità (precisamente un resto) piccolissima, infinitesima, chiamata o-piccolo, che viene fuori dallo sviluppo.
Il binomio di Newton non è solamente una formula di gran utilità, ma anche di gran fascino, al punto che il poeta portoghese Fernando Pessoa (1888-1935), nell'opera Una sola moltitudine, scrisse:
"Il binomio di Newton è bello come la Venere di Milo, peccato che pochi se ne accorgano"
Ritorniamo all'integrale
.gif)
La radice quadrata di (1 - x) si può dunque riscrivere sfruttando il binomio di Newton.
C'è solo un piccolo problema: il segno meno.
Come si fa ad ovviare a tale inconveniente?
Semplice, poniamo

in modo da ricondurci alla forma

la quale si sviluppa come:
Come si può constatare, nel caso di un esponente non naturale, lo sviluppo binomiale genera una somma infinita di termini (una serie).
Esplicitiamo i coefficienti binomiali:



Pertanto abbiamo:
Ricordando che
Possiamo finalmente dire che
Ciò ci permette di scrivere il nostro integrale come:
ovvero:
Integrando termine a termine si ottiene che l'area A è uguale a:
Newton si rese poi conto che quest'area A è anche l'area del settore circolare DAC meno l'area del triangolo rettangolo DBC (in figura).
L'area di un triangolo rettangolo è pari al prodotto dei cateti diviso 2.
Ergo:

Per quanto riguarda il settore circolare, al fine di determinare la sua area, Newton ragionò ancora sul triangolo.
In effetti, il triangolo DBC è un particolare tipo di triangolo rettangolo, dato che la lunghezza di un suo cateto è pari a metà di quella dell'ipotenusa.
Ne consegue che gli angoli interni del triangolo hanno valori 90°, 60° e 30°.

Dunque l'angolo al centro del settore circolare è semplicemente pari a 60°, ossia un terzo dell'angolo piatto che forma il semicerchio.
Newton si accorse quindi che l'area del settore circolare era equivalente a un terzo dell'area del semicerchio.
In simboli:
Ne deriva che:
Non resta che uguagliare le 2 espressioni dell'area A rinvenute con metodi diversi:
Il che porta a trovare la seguente espressione di pi greco:
Newton utilizzò la suddetta formula, nel 1666, per calcolare ben 15 cifre decimali di pi greco.
Concludo augurandovi anticipatamente un buon Pi Day!


.gif)
.gif)

.gif)




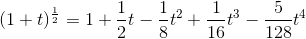


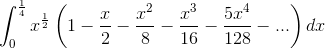




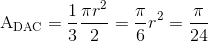











.gif)







Nessun commento:
Posta un commento